
 ,且点P(-2,0)在椭圆C上.
,且点P(-2,0)在椭圆C上. ,
, ,a=2,所以c=
,a=2,所以c= ,
, ;
;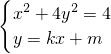 ,得(1+4k2)x2+8kmx+4(m2-1)=0,
,得(1+4k2)x2+8kmx+4(m2-1)=0,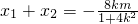 ,
,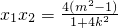 ,
,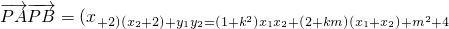 =
=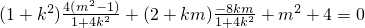 ,
,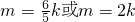 ,
,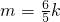 时,
时,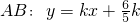 恒过定点
恒过定点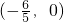 ;
;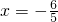 ,则AB与椭圆C相交于
,则AB与椭圆C相交于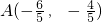 ,
,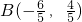 ,
,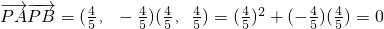 ,∵PA⊥PB,满足题意,
,∵PA⊥PB,满足题意,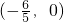 .
. ,由题意得
,由题意得 ,a=2,再由b2=a2-c2可求得c,b;
,a=2,再由b2=a2-c2可求得c,b; =0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB:
=0可得m,k的关系式,分别代入直线方程可求得定点坐标,②当直线l垂直于x轴时,直线AB: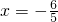 ,检验即可;
,检验即可;

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:单选题
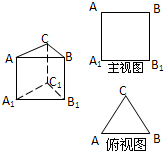 如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,主视图是边长为2的正方形,则该三棱柱的左视图周长为
如图,水平放置的三棱柱的侧棱长和底面边长均为2,且侧棱AA1⊥平面A1B1C1,主视图是边长为2的正方形,则该三棱柱的左视图周长为

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第 ________行.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第n次全行的数都为1的是第 ________行.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
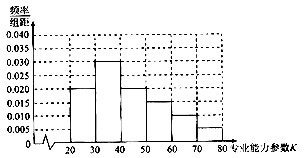
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com