
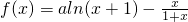 在[0,+∞)上单调递增,数列{an}满足
在[0,+∞)上单调递增,数列{an}满足 ,
,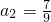 ,
,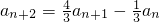 (n∈N*).
(n∈N*).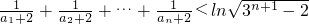 (n∈N*).
(n∈N*).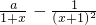 ≥0在[0,+∞)上恒成立
≥0在[0,+∞)上恒成立 在[0,+∞)上恒成立
在[0,+∞)上恒成立 ∈(0,1]
∈(0,1]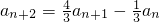 ,
,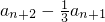 =
=
 }是常数数列
}是常数数列 ,
,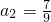 ,
,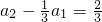
 =
=
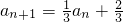
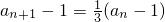
 ,公比为
,公比为 的等比数列
的等比数列 )•
)•
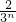 ;
;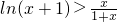 对x∈[0,+∞)恒成立
对x∈[0,+∞)恒成立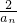 ,则
,则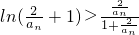
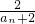 <ln(
<ln(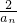 +1)=ln(3n+1-2)-ln(3n-2)
+1)=ln(3n+1-2)-ln(3n-2)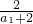 +
+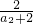 +…+
+…+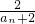 <[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)
<[ln(32-2)-ln(31-2)]+[ln(33-2)-ln(32-2)]+…+ln(3n+1-2)-ln(3n-2)=ln(3n+1-2)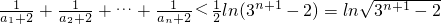
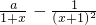 ≥0在[0,+∞)上恒成立,分离参数,可得a≥
≥0在[0,+∞)上恒成立,分离参数,可得a≥ 在[0,+∞)上恒成立,求出最值,即可得到结论;
在[0,+∞)上恒成立,求出最值,即可得到结论; }是常数数列,再证明{an-1}是首项为-
}是常数数列,再证明{an-1}是首项为- ,公比为
,公比为 的等比数列,即可求数列{an}的通项公式;
的等比数列,即可求数列{an}的通项公式;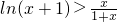 对x∈[0,+∞)恒成立,令x=
对x∈[0,+∞)恒成立,令x=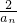 ,则
,则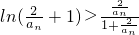 ,可得
,可得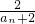 <ln(3n+1-2)-ln(3n-2),叠加即可证得结论.
<ln(3n+1-2)-ln(3n-2),叠加即可证得结论.

 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
(本小题满分14分)已知函数![]() 在(0,+
在(0,+![]() )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程![]() 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.
(1)求c的值;(2)求证:![]() ;(3)求|α–β|的取值范围.
;(3)求|α–β|的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省7校高三联考理数试题 题型:填空题
(本小题满分12分)
已知函数 在[0,+
在[0,+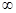 )上最小值是
)上最小值是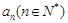
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求证:
,求证: ;
;
查看答案和解析>>
科目:高中数学 来源:2014届天津市高一上学期期中考试数学 题型:选择题
已知函数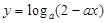 在[0,1]上是
在[0,1]上是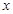 的减函数,则
的减函数,则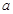 的取值范围是(
)
的取值范围是(
)
A.(0,1) B.(0,2) C.(1,2) D.[2,+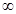 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com