
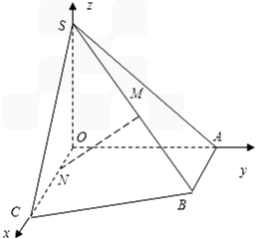
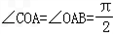 ,OA=OS=AB=1,OC=2,点M是棱SB的中点,N是OC上的点,且ON:NC=1:3.
,OA=OS=AB=1,OC=2,点M是棱SB的中点,N是OC上的点,且ON:NC=1:3.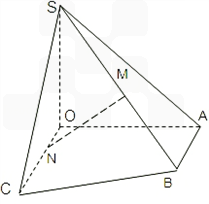
 ,0,0),M(
,0,0),M(  ,
, ,
,  )
)  =(0,﹣
=(0,﹣  ,﹣
,﹣ ),
),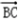 =(1,﹣1,0)
=(1,﹣1,0)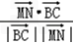 =
=
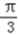 ;
; =(a,b,c)
=(a,b,c)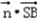 =(a,b,c)·(1,1,﹣1)=a+b﹣c=0
=(a,b,c)·(1,1,﹣1)=a+b﹣c=0 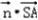 =(a,b,c)·(0,1,﹣1)=b﹣c=0
=(a,b,c)·(0,1,﹣1)=b﹣c=0  =(0,1,1)
=(0,1,1)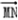 =(0,﹣
=(0,﹣  ,﹣
,﹣ ),
), 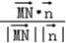 |=
|= 
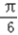


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
(1)如图所示,给出两块面积相同的正三角形纸片(如图(1),图(2))要求用其中一块剪拼成一个正三棱柱模型,另一块剪拼成一个正三棱锥模型,使它们的全面积都相等,请设计一种剪拼方法,分别用虚线标示在图(1)、图(2)中,并作简要说明:

(2)(本小题为附加题)如果给出的是一块任意三角形纸片(如图(3)).要求剪拼成一个直三棱柱模型,全面积与给出的三角形的面积相等,请设计一种剪拼方法,作虚线表示在图(3)中,并作简要说明.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省南京市高三上学期期中考试数学试题 题型:解答题
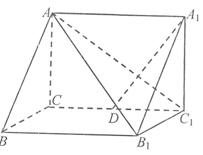
附加题) 如图所示,在直三棱柱ABC—A1B1C1中, D是棱CC1的中点。
D是棱CC1的中点。
(1)证明:A1D⊥平面AB1C1;
(2)求二面角B—AB1—C1的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com