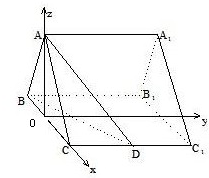
分析:(1)取BC中点O,连接AO,DO,则∠ADO是直线AD与侧面BB1C1C成角,由此利用题设条件能求出此正三棱柱侧棱CC1长.
(2)以OC为x轴,以过O点平行于CC1的直线为y轴,以OA为z轴,建立空间直角坐标系,用向量法能求出二面角A-BD-C的正切值.
解答:
解:(1)取BC中点O,连接AO,DO,则∠ADO是直线AD与侧面BB
1C
1C成角,
∵三棱柱ABC-A
1B
1C
1中,底面是边长为2的正三角形,
∴AO=
=
,
∵D是侧棱CC
1中点,直线AD与侧面BB
1C
1C成角为45°,
∴CD=
=
,
∴CC
1=2DC=2
.
(2)以OC为x轴,以过O点平行于CC
1的直线为y轴,以OA为z轴,建立空间直角坐标系,
则A(0,0,
),B(-1,0,0),C(1,0,0),D(1,
,0),
∴
=(-1,0,-),
=(1,
,-
),
设
=(x,y,z)是平面ABD的一个法向量,则
•=0,
•=0,
∴
,解得
=(
,-
,-1)
设二面角A-BD-C的平面角为θ,
∵面BCD的一个法向量是
=(0,0,
),
∴cosθ=|cos<
,
>|=|
|=
.
∴tanθ=3.
故二面角A-BD-C的正切值为3.
点评:本题考查三棱柱侧棱长的求地,考查二面角正切值的求法,解决此类问题的关键是熟悉几何体的结构特征,建立适当的空间直角坐标系进而利用空间向量解决空间中的空间角与空间距离问题.

 三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱CC1,AA1,BB1都与左右的两个底面垂直,D是侧棱CC1中点,直线AD与侧面BB1C1C成角为45°.
三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱CC1,AA1,BB1都与左右的两个底面垂直,D是侧棱CC1中点,直线AD与侧面BB1C1C成角为45°. 解:(1)取BC中点O,连接AO,DO,则∠ADO是直线AD与侧面BB1C1C成角,
解:(1)取BC中点O,连接AO,DO,则∠ADO是直线AD与侧面BB1C1C成角,


 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=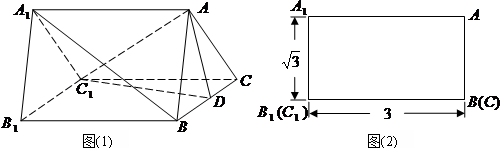
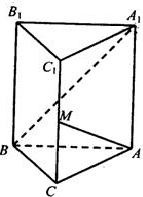 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1= 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.