
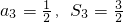 ,则首项a1=________.
,则首项a1=________. 或2
或2 ,又得到关于首项和公比的关系式,记作②,①÷②消去首项,得到关于q的方程,求出方程的解即可得到q的值,把q的值代入①即可求出首项a1的值.
,又得到关于首项和公比的关系式,记作②,①÷②消去首项,得到关于q的方程,求出方程的解即可得到q的值,把q的值代入①即可求出首项a1的值. ,a3=
,a3= ,
, ②,
②, =2,
=2, 或q=1,
或q=1, 代入①,解得a1=2;把q=1代入①,解得a1=
代入①,解得a1=2;把q=1代入①,解得a1= ,
, 或2.
或2. 或2
或2

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com