两异面直线a,b成80°角,过空间任意一点P作直线l,使其与两直线a,b成等角50°,则这样的直线l有 条.
【答案】
分析:根据已知中异面直线a与b所成的角为80°,设O为空间一点,过O分别作OA∥a,OB∥b,则OA,OB成80°角.过O点作出直线OA,OB相交所成角的两条角平分线,满足题意的直线或为两平分线或其射影为两平分线,由此确定直线条数.
解答:解:首先给出两个性质①与一个角∠AOB的两边成等角的直线在面AOB内的射影是∠AOB的平分线.
②若∠AOC所在平面与∠BOC所在平面垂直,则有cos∠AOCcos∠BOC=cos∠AOB.
在空间任取一点O,作OA∥a,OB∥b,则OA,OB成80°角,不妨设∠AOB=80°,如图
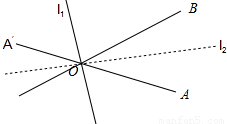
(1)直线l
1为∠AOB的补角∠A′OB=100°的平分线,此时l
1与两直线 OA,OB成等角50°,从而l
1与两直线a,b成等角50°,若把直线l
1绕O在垂直于面A′OB 的平面内旋转时,设
l
1与面A′OB所成的角为θ,由性质②cosθcos50°=cos50°,θ=0°,与旋转前l
1重合. 即此时只有一条直线满足题意.
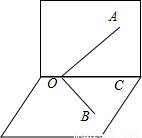
(2)直线l
2为∠AOB的平分线,显然l
2与两直线 OA,OB成等角40°,若把直线l
2绕O在垂直于面AOB 的平面内旋转时,设l
2与面AOB所成的角为θ,由性质②cosθcos40°=cos50°,
移向得出cosθ=
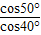
<1.存在θ,根据对称性,在面AOB两侧各有一条.即此时共有两条直线满足题意.
综上所述这样的直线l有3条.
故答案为:3.
点评:本题考查异面直线所成的角,以及解决异面直线所成的角的方法(平移法)的应用,体现了转化的思想和运动变化的思想方法. 本题利用定量的方法进行问题解决,当改变题干中两个角的度数大小时,此法照样使用.



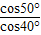 <1.存在θ,根据对称性,在面AOB两侧各有一条.即此时共有两条直线满足题意.
<1.存在θ,根据对称性,在面AOB两侧各有一条.即此时共有两条直线满足题意.

 角的异面直线的对数为
角的异面直线的对数为