
| 25 |
| 3 |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
| px+1 |
| x+1 |
| 1 |
| 2 |
| n |
| cn |
| -1 |
| anSn2 |
查看答案和解析>>
科目:高中数学 来源:导练必修一数学苏教版 苏教版 题型:022
函数的概念
设A,B是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个x,在集合B中都有________的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的函数,记作y=f(x),x∈A.
其中x叫________,x的取值范围A叫做函数y=f(x)的________;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}(![]() B)叫做函数y=f(x)的________.函数符号y=f(x)表示“y是x的函数”,有时简记作函数________.
B)叫做函数y=f(x)的________.函数符号y=f(x)表示“y是x的函数”,有时简记作函数________.
(1)函数实际上就是集合A到集合B的一个特殊对应f:A→B,这里A、B为________的数集.
(2)A:定义域;{f(x)|x∈A}:值域,其中{f(x)|x∈A}________B;f:对应法则,x∈A,y∈B.
(3)函数符号:y=f(x)y是x的函数,简记f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)函数的三要素:函数由 、 以及从定义域到值域的 三部分组成的特殊的映射.?
(3)函数的表示法: 、 、 .
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉市蔡甸二中高三(下)第五次月考数学试卷(文科)(解析版) 题型:解答题
 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+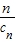 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2008年上海市八区联考高考数学模拟试卷(理科)(解析版) 题型:解答题
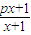 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+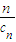 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;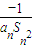 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com