
 �ס�����λͬѧ��5�ο����е���ѧ�ɼ��þ�Ҷͼ��ʾ��ͼ���м�һ�е����ֱ�ʾ��ѧ�ɼ���ʮλ���֣����ߵ����ֱ�ʾ��ѧ�ɼ��ĸ�λ���֣����ס������˵�ƽ���ɼ��ֱ���$\overline{{x}_{1}}$��$\overline{{x}_{2}}$��������˵����ȷ���ǣ�������
�ס�����λͬѧ��5�ο����е���ѧ�ɼ��þ�Ҷͼ��ʾ��ͼ���м�һ�е����ֱ�ʾ��ѧ�ɼ���ʮλ���֣����ߵ����ֱ�ʾ��ѧ�ɼ��ĸ�λ���֣����ס������˵�ƽ���ɼ��ֱ���$\overline{{x}_{1}}$��$\overline{{x}_{2}}$��������˵����ȷ���ǣ�������| A�� | $\overline{{x}_{1}}��\overline{{x}_{2}}$���ױ��ҳɼ��ȶ� | B�� | $\overline{{x}_{1}}��\overline{{x}_{2}}$���ұȼ׳ɼ��ȶ� | ||
| C�� | $\overline{{x}_{1}}��\overline{{x}_{2}}$���ױ��ҳɼ��ȶ� | D�� | $\overline{{x}_{1}}��\overline{{x}_{2}}$���ұȼ׳ɼ��ȶ� |
���� �ɾ�Ҷͼ�ֱ����$\overline{{x}_{1}}$��$\overline{{x}_{2}}$���Ӷ��õ�$\overline{{x}_{1}}��\overline{{x}_{2}}$���ɾ�Ҷͼ֪�����ݽϷ�ɢ���ҵ����ݽϼ��У��Ӷ��õ��ұȼ׳ɼ��ȶ���
��� �⣺�ɾ�Ҷͼ֪��
$\overline{{x}_{1}}$=$\frac{1}{5}$��72+77+78+86+92��=81��
$\overline{{x}_{2}}$=$\frac{1}{5}$��78+88+88+91+90��=87��
��$\overline{{x}_{1}}��\overline{{x}_{2}}$��
�ɾ�Ҷͼ֪�����ݽϷ�ɢ���ҵ����ݽϼ��У�
���ұȼ׳ɼ��ȶ���
��ѡ��B��
���� ���⿼���������ݵ�ƽ�������ȶ��Ե��жϣ��ǻ����⣬����ʱҪ�������⣬ע�⾥Ҷͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��23��10�����ɶ���λ������10111��2�� | |
| B�� | �ڿռ�����ϵ��M��1��2��3������x��ĶԳƵ�Ϊ��1��-2��-3�� | |
| C�� | ���ݣ�2��4��6��8�ķ��������ݣ�1��2��3��4�ķ����2�� | |
| D�� | ����A��-1��0����Բx2+y2-mx+1=0���ⲿ����m��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
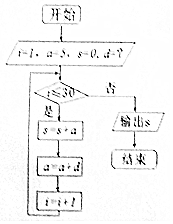 ������������֮������ѧ���������е�֪ʶ��������⣮��Ԫ5�����й��Ŵ����ݷḻ����ѧ�����������㾭����������Ϊ��������Ů��֯�����湦��������֯��ߣ���һ��֯��ƥ���ɣ������漸�Σ�������������˼����Ƶ�һ�������ͼ��ͼ���������SֵΪ��ƥ���ɣ�һƥ=4�ɣ�һ��=10�ߣ������ͼ��dΪ��������
������������֮������ѧ���������е�֪ʶ��������⣮��Ԫ5�����й��Ŵ����ݷḻ����ѧ�����������㾭����������Ϊ��������Ů��֯�����湦��������֯��ߣ���һ��֯��ƥ���ɣ������漸�Σ�������������˼����Ƶ�һ�������ͼ��ͼ���������SֵΪ��ƥ���ɣ�һƥ=4�ɣ�һ��=10�ߣ������ͼ��dΪ��������| A�� | $\frac{1}{2}$�� | B�� | $\frac{8}{15}$�� | C�� | $\frac{16}{31}$�� | D�� | $\frac{16}{29}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{1}{{e}^{2}}$��+�ޣ� | B�� | ��-1��$\frac{1}{{e}^{2}}$] | C�� | [-$\frac{1}{{e}^{2}}$��1�� | D�� | ��-�ޣ�-$\frac{1}{{e}^{2}}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 0 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com