
对于函数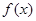 ,若存在
,若存在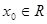 ,使
,使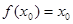 成立,则称
成立,则称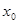 为
为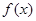 的不动点. 已知函数
的不动点. 已知函数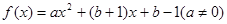 ,若对任意实数b,函数
,若对任意实数b,函数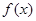 恒有两个相异的不动点,则实数
恒有两个相异的不动点,则实数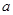 的取值范围是 ( )
的取值范围是 ( )
A.(0,1) B.(1,+∞) C.[0,1) D.以上都不对
A
【解析】
试题分析:转化为ax2+bx+b-1=0有两个不等实根,转化为b2-4a(b-1)>0恒成立,再利用二次函数大于0恒成立须满足的条件来求解即可.
根据题意可知,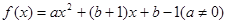 ,
,
对任意实数b,函数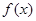 恒有两个相异的不动点
恒有两个相异的不动点
即f(x)=ax2+(b+1)x+b-1=x有两个不等实根,
转化为ax2+bx+b-1=0有两个不等实根,须有判别式大于0恒成立
即b2-4a(b-1)>0?△=(-4a)2-4×4a<0?0<a<1,
∴a的取值范围为0<a<1;
考点:本试题考查了函数的零点问题。
点评:解决该试题的关键是理解不动点的定义,进而转化为方程有无实数根来分析,那么体现了等价转化的思想的运用。属于基础题。


科目:高中数学 来源:2012届湖南省涟源一中高三第四次月考理科数学试卷 题型:解答题
对于函数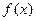 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称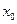 为
为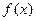 的不动点.如果函数
的不动点.如果函数 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且 .
.
(1) 求函数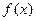 的单调区间;
的单调区间;
(2) 已知数列 各项不为零且不为1,满足
各项不为零且不为1,满足 ,求证:
,求证: ;
;
设 ,
, 为数列
为数列 的前
的前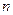 项和,求证:
项和,求证: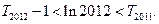
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第一次调研考试理科数学试卷(解析版) 题型:解答题
对于函数 ,若存在
,若存在 ,使
,使 ,则称
,则称 是
是 的一
的一
个"不动点".已知二次函数
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)对任意实数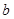 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求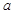 的取值范围;
的取值范围;
(3)在(2)的条件下,若 的图象上
的图象上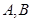 两点的横坐标是
两点的横坐标是 的不动点,
的不动点,
且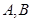 两点关于直线
两点关于直线 对称,求
对称,求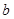 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省高三第四次月考理科数学试卷 题型:解答题
对于函数 ,若存在
,若存在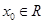 ,使
,使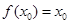 成立,则称
成立,则称 为
为 的不动点.如果函数
的不动点.如果函数 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且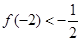 .
.
(1)
求函数 的单调区间;
的单调区间;
(2)
已知数列 各项不为零且不为1,满足
各项不为零且不为1,满足 ,求证:
,求证: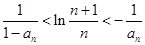 ;
;
设 ,
, 为数列
为数列 的前
的前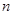 项和,求证:
项和,求证:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第二次月考试卷理科数学 题型:解答题
(本小题满分14分)对于函数 ,若存在
,若存在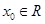 ,使
,使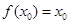 成立,则称
成立,则称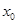 为
为 的不动点。如果函数
的不动点。如果函数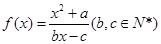 有且仅有两个不动点
有且仅有两个不动点 、
、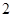 ,且
,且
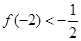 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列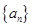 满足
满足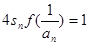 ,求证:
,求证: ;
;
(3)设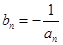 ,
,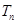 为数列
为数列 的前
的前 项和,求证:
项和,求证: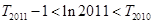 。
。
查看答案和解析>>
科目:高中数学 来源:云南省2010-2011学年高三数学一轮复习测试:函数(1) 题型:解答题
对于函数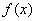 ,若存在
,若存在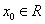 ,使
,使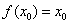 成立,则称
成立,则称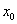 为
为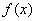 的不动点.如果函数
的不动点.如果函数 有且仅有两个不动点
有且仅有两个不动点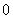 、
、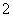 ,且
,且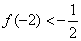 .试求函数
.试求函数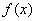 的单调区间;
的单调区间;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com