Question

已知直线y=ax+1与双曲线3x²-y²=1交于不同的两点A、B.

(1)求实数a的取值范围.

(2)是否存在这样的实数a,使A、B两点关于直线y=x对称?若存在,求出a的值;若不存在,请说明理由.

Answer 1

思路分析:(1)由于直线与双曲线交于不同的两点A、B,利用判别式可确定a的取值范围,为(2)中判定a值的存在性打下基础;

(2)点——线——点的对称问题中,一定要注意应用“垂直且平分”这个条件.

解:(1)由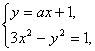得

(3-a²)x²-2ax-2=0.                                                            (*)

由题意可得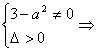-＜a＜,且a≠±.

(2)假设存在实数a,使A、B两点关于直线y=x对称,则设A(x₁,y₁)、B(x₂,y₂),

由题意可得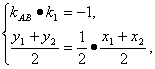

即

∴x₁+x₂=.

设AB的中点为M(x₀,y₀),则x₀=.

又∵点M(x₀,y₀)在直线y=x上,

∴y₀=,即M(,).

又由(1)知x₁+x₂=,

当x₁+x₂=时,求得a=,与a=-2不符.

故不存在实数a使A、B两点关于直线y=x对称.