
(本小题满分13分)已知矩形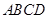 的对角线交于点
的对角线交于点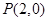 ,边
,边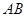 所在直线的方程为
所在直线的方程为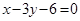 ,点
,点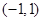 在边
在边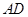 所在的直线上,
所在的直线上,
(1)求矩形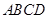 的外接圆的方程;
的外接圆的方程;
(2)已知直线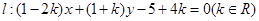 ,求证:直线
,求证:直线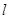 与矩形
与矩形 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线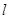 的方程.
的方程.
解:(1)由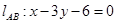 且
且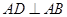 ,点
,点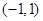 在边
在边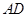 所在的直线上
所在的直线上
 所在直线的方程是:
所在直线的方程是: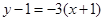 即
即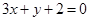 由
由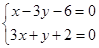 得
得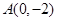
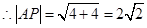
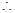 矩形ABCD的外接圆的方程是:
矩形ABCD的外接圆的方程是: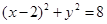
(2)直线 的方程可化为:
的方程可化为: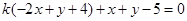
 可看作是过直线
可看作是过直线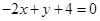 和
和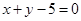 的交点
的交点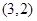 的直线系,即
的直线系,即 恒过定点
恒过定点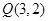 由
由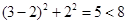 知点
知点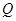 在圆
在圆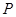 内,所以
内,所以 与圆
与圆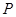 恒相交,
恒相交,
设 与圆
与圆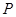 的交点为
的交点为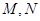 ,
,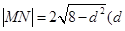 为
为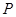 到
到 的距离)
的距离)
设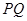 与
与 的夹角为
的夹角为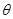 ,则
,则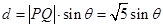 当
当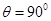 时,
时,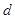 最大,
最大,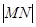 最短此时
最短此时 的斜率为
的斜率为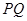 的斜率的负倒数:
的斜率的负倒数: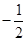 ,
, 的方程为
的方程为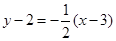
即 :
:
【解析】本试题主要是考查了直线方程和圆的方程的求解,以及直线与圆的位置关系的综合运用。
(1) 矩形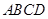 的对角线交于点
的对角线交于点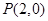 ,边
,边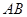 所在直线的方程为
所在直线的方程为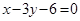 ,点
,点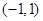 在边
在边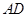 所在的直线上,得到圆心坐标和半径从而得到圆的方程。
所在的直线上,得到圆心坐标和半径从而得到圆的方程。
(2)直线 的方程可化为:
的方程可化为: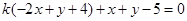
 可看作是过直线
可看作是过直线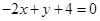 和
和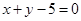 的交点
的交点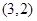 的直线系,即
的直线系,即 恒过定点
恒过定点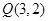 由
由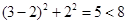 知点
知点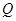 在圆
在圆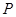 内,所以
内,所以 与圆
与圆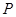 恒相交,
恒相交,
设 与圆
与圆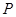 的交点为
的交点为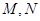 ,
,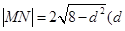 为
为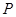 到
到 的距离)借助于斜率的关系式得到结论。
的距离)借助于斜率的关系式得到结论。
解:(1)由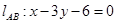 且
且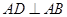 ,点
,点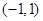 在边
在边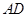 所在的直线上
所在的直线上
 所在直线的方程是:
所在直线的方程是: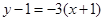 即
即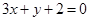 由
由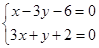 得
得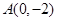
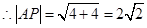
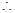 矩形ABCD的外接圆的方程是:
矩形ABCD的外接圆的方程是: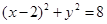
(2)直线 的方程可化为:
的方程可化为: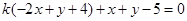
 可看作是过直线
可看作是过直线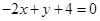 和
和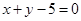 的交点
的交点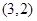 的直线系,即
的直线系,即 恒过定点
恒过定点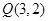 由
由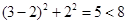 知点
知点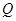 在圆
在圆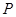 内,所以
内,所以 与圆
与圆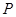 恒相交,
恒相交,
设 与圆
与圆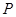 的交点为
的交点为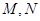 ,
,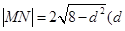 为
为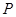 到
到 的距离)
的距离)
设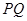 与
与 的夹角为
的夹角为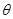 ,则
,则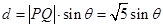 当
当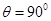 时,
时,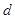 最大,
最大,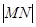 最短此时
最短此时 的斜率为
的斜率为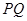 的斜率的负倒数:
的斜率的负倒数: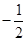 ,
, 的方程为
的方程为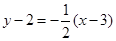
即 :
:


科目:高中数学 来源:2015届江西省高一第二次月考数学试卷(解析版) 题型:解答题
(本小题满分13分)已知函数
 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数 在区间
在区间 上的图象.
上的图象.
(3)设0<x< ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三年级八月份月考试卷理科数学 题型:解答题
(本小题满分13分)已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性;
(3)若对任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:河南省09-10学年高二下学期期末数学试题(理科) 题型:解答题
(本小题满分13分)如图,正三棱柱 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求异面直线 与
与 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[来源:KS5
U.COM
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
(本小题满分13分)
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
.
(1) 求函数 的表达式;
的表达式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面积
的面积
(3) 求数列 的前
的前 项和
项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com