Question

已知正三棱台上底边为3，下底边为6，高为1，求斜高与侧棱长．

Answer 1

分析：连接上下底面中心OO₁，令C，D为同一侧面上上下底边的中点，过BC做底面的垂线，垂足分别为EF，则E，F均在AD上，结合棱台上底边为3，下底边为6，高为1，利用勾股定理可得答案．

解答：解：如图画出正三棱台，连接上下底面中心OO₁，
令C，D为同一侧面上上下底边的中点，
过BC做底面的垂线，垂足分别为EF，则E，F均在AD上，

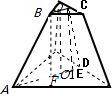
∵正三棱台上底边为3，下底边为6，高为1，
∴OC=

3

2

，O₁D=

3

，CE=1，
则斜高为

12+( 3 - 3 2 )2

=

7

2

，
且OB=

3

，O₁A=2

3

，BF=1，
则侧棱长为

12+(2 3 - 3 )2

=2

点评：本题考查的知识点是棱台的结构特征，其中构造直角三角形将问题转化为利用勾股定理求解直角三角形是解答问题的关键．