
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使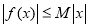 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:①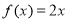 :②
:② :③
:③ ;④
;④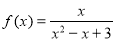 ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切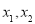 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
A.1个 B.2个 C..3个 D.4个
C
【解析】
试题分析:【解析】
①对于函数 ,存在
,存在 ,使
,使 对 一切实数x均成 立,所以该函数是“倍约束函数”;
对 一切实数x均成 立,所以该函数是“倍约束函数”;
②对于函数 ,当
,当 时,
时, ,故不存在常数M>0,使
,故不存在常数M>0,使 对 一切实数x均成 立,所以该函数不是“倍约束函数”;
对 一切实数x均成 立,所以该函数不是“倍约束函数”;
③对于函数 ,当
,当 时,
时, ,故不存在常数M>0,使
,故不存在常数M>0,使 对 一切实数x均成 立,所以该函数不是“倍约束函数”;
对 一切实数x均成 立,所以该函数不是“倍约束函数”;
④对于函数 ,因为当
,因为当 时,
时, ;
;
当 时,
时, ,所以存在常数
,所以存在常数 ,使
,使 对 一切实数x均成 立, 所以该函数是“倍约束函数”;
对 一切实数x均成 立, 所以该函数是“倍约束函数”;
⑤由题设 是定义在实数集R上的奇函数,
是定义在实数集R上的奇函数, ,所以在
,所以在 中令
中令 ,于是有
,于是有 ,即存在常数
,即存在常数 ,使
,使 对 一切实数x均成 立, 所以该函数是“倍约束函数”;
对 一切实数x均成 立, 所以该函数是“倍约束函数”;
综上可知“倍约束函数”的有①④⑤共三个,所以应选C.
考点:1、新定义;2、赋值法;3、基本初等函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年天津市红桥区高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
己知a∈R,函数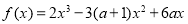
(1)若a=1,求曲线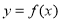 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;
(2)若|a|>1,求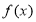 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)文科数学试卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,侧面PAD 底面ABCD,侧棱
底面ABCD,侧棱 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.
(1)求证:PE 平面ABCD:
平面ABCD:
(2)求异面直线PB与CD所成角的余弦值:
(3)求点A到平面PCD的距离.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷理科数学试卷(解析版) 题型:解答题
已知函数
(1)若函数 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件;
(3)若函数 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷文科数学试卷(解析版) 题型:解答题
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模理科数学试卷(解析版) 题型:解答题
给定椭圆 .称圆心在原点O,半径为
.称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线 ,使得
,使得 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断 是否垂直?并说明理由.
是否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD的中点.若 =2,
=2, =1,且
=1,且 BAD=60o,则
BAD=60o,则  。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com