
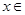
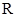 ,用符号
,用符号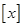 表示不超过
表示不超过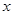 的最大整数。函数
的最大整数。函数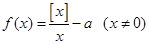 有且仅有3个零点,则
有且仅有3个零点,则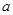 的取值范围是__________.
的取值范围是__________.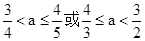
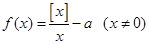 ,所以
,所以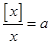 ;
;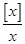 =0;
=0;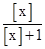 <
<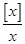 ≤1,即
≤1,即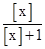 <a≤1。
<a≤1。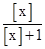 随着[x]的增大而增大。
随着[x]的增大而增大。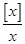 ≥1;
≥1;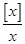 <
<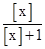 ,即1≤a<
,即1≤a<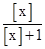 ,
,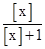 随着[x]的减小而增大。
随着[x]的减小而增大。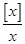 -a有且仅有3个零点,只能使[x]=1,2,3;或[x]=-1,-2,-3。
-a有且仅有3个零点,只能使[x]=1,2,3;或[x]=-1,-2,-3。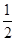 <a≤1;
<a≤1;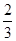 <a≤1;
<a≤1;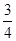 <a≤1;
<a≤1;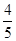 <a≤1;
<a≤1;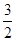 ;
;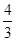 ;综上所述,
;综上所述,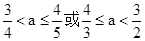


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
A.f(x)=x与g(x)=(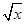 )2 )2 | B.f(x)=|x|与g(x)= |
C.f(x)=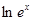 与g(x)= 与g(x)=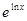 | D.f(x)=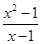 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
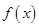 满足
满足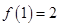 ,且当
,且当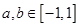 ,
,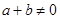 时,有
时,有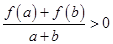 .
.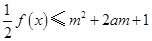 对所有
对所有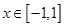 ,
,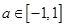 恒成立,
恒成立,查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
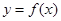 在区间
在区间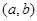 上的导函数为
上的导函数为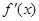 ,
,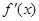 在区间
在区间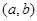 上的导函数为
上的导函数为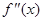 ,若在区间
,若在区间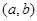 上
上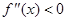 恒成立,则称函数
恒成立,则称函数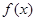 在区间
在区间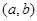 上的“凸函数”。已知
上的“凸函数”。已知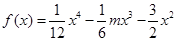 ,若对任意的实数
,若对任意的实数 满足
满足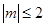 时,函数
时,函数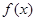 在区间
在区间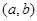 上为“凸函数”,则
上为“凸函数”,则 的最大值为
的最大值为查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
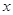 元.
元.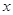 值;(6分)
值;(6分)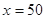 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)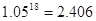 ,
,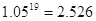 ,
, ,
, 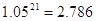 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com