
| 3 |
| 5 |
| C33 |
| C63 |
| 1 |
| 20 |
| C32C31 |
| C63 |
| 9 |
| 20 |
| C31C32 |
| C63 |
| 9 |
| 20 |
| C33 |
| C63 |
| 1 |
| 20 |
| X | 0 | 10 | 20 | 30 | ||||||||
| P |
|
|
|
|
| 1 |
| 20 |
| 9 |
| 20 |
| 9 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
| 9 |
| 20 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 81 |
| 125 |
| 1 |
| 2 |
| 81 |
| 125 |
| 22 |
| 125 |
| 22 |
| 125 |
| 103 |
| 125 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
| 3 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 5 |
查看答案和解析>>
科目:高中数学 来源:2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷(解析版) 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是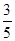 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三高考模拟考试(八)理科数学试卷(解析版) 题型:解答题
甲、乙两人参加某种选拔测试.在备选的 道题中,甲答对其中每道题的概率都是
道题中,甲答对其中每道题的概率都是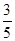 ,乙能答对其中的
,乙能答对其中的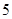 道题.规定每次考试都从备选的
道题.规定每次考试都从备选的 道题中随机抽出
道题中随机抽出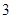 道题进行测试,答对一题加
道题进行测试,答对一题加 分,答错一题(不答视为答错)减
分,答错一题(不答视为答错)减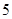 分,至少得
分,至少得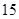 分才能入选.
分才能入选.
(1)求甲得分的数学期望;
(2)求甲、乙两人同时入选的概率.
查看答案和解析>>
科目:高中数学 来源:2012年北京市西城区高考数学二模试卷(理科)(解析版) 题型:解答题
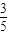 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com