【答案】
分析:根据圆锥曲线的性质逐一判断,①应用斜率的几何意义,把
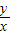
看成点(x,y)与点(0,0)连线的斜率,即可通过求圆的切线斜率来计算;②椭圆的离心率e=
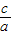
,所以要判断两个椭圆的离心率是否相同,只需求出两个椭圆中的a,c的值;③要求双曲线的焦点坐标,必须求出c的值以及焦点所在坐标轴;④直线与圆若没有公共点,这直线与圆相离,圆心到直线的距离大于半径;⑤要求离心率的范围,只需用含参数a的式子表示离心率,再根据a的范围求出e的范围.
解答:解:①
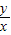
=
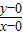
,可看成点(x,y)与点(0,0)连线的斜率,也即圆(x-2)
2+y
2=3上点与坐标原点连线的斜率.
∴
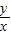
的最值即为过原点的直线与圆相切时该直线的斜率,设过原点的圆的切线方程为y=kx,即kx-y=0,
圆(x-2)
2+y
2=3的圆心(2,0)到直线kx-y=0的距离
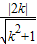
=
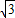
,解得k=±

,∴
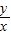
的最大值为
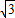
,∴①正确.
②椭圆
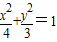
中a=2,c=1,∴离心率为

,椭圆
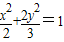
中a=
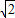
,c=
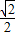
,∴离心率为

,∴②正确.
③∵双曲线方程为
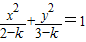
,∴(2-k)(3-k)<0,∴2<k<3,∴2-k<0.3-k>0,∴双曲线的焦点在y轴上,
且c
2=3-k+k-2=1,∴c=1,∴焦点坐标为(0,±1),∴③错误.
④若圆x
2+y
2=1与直线y=kx+2没有公共点,则圆心到直线的距离大于半径,即
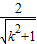
>1,解得,-
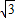
<k<
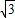
,若-
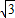
<k<
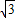
,则圆心到直线的距离大于半径,∴圆与直线无公共点,∴圆x
2+y
2=1与直线y=kx+2没有 公共点的充要条件是
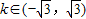
,∴④正确.
⑤∵双曲线方程为
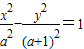
,∴c
2=a
2+(a+1)
2,
∴e
2=
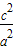
=
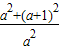
=
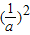
+
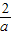
+2=

+1,∵a>1,∴0<

<1,
∴2<e
2<5,∴

<e<
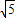
∴⑤正确.
故选D
点评:本题主要考查圆锥曲线的一些性质,因为是多选题,只需逐个判断即可.

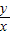 的最大值为
的最大值为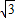 ;②椭圆
;②椭圆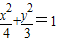 与椭圆
与椭圆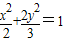 有相同的离心率;③双曲线
有相同的离心率;③双曲线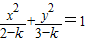 的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是
的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是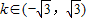 ⑤设a>1,则双曲线
⑤设a>1,则双曲线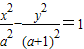 的离心率e的取值范围是
的离心率e的取值范围是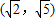 .
.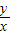 看成点(x,y)与点(0,0)连线的斜率,即可通过求圆的切线斜率来计算;②椭圆的离心率e=
看成点(x,y)与点(0,0)连线的斜率,即可通过求圆的切线斜率来计算;②椭圆的离心率e=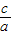 ,所以要判断两个椭圆的离心率是否相同,只需求出两个椭圆中的a,c的值;③要求双曲线的焦点坐标,必须求出c的值以及焦点所在坐标轴;④直线与圆若没有公共点,这直线与圆相离,圆心到直线的距离大于半径;⑤要求离心率的范围,只需用含参数a的式子表示离心率,再根据a的范围求出e的范围.
,所以要判断两个椭圆的离心率是否相同,只需求出两个椭圆中的a,c的值;③要求双曲线的焦点坐标,必须求出c的值以及焦点所在坐标轴;④直线与圆若没有公共点,这直线与圆相离,圆心到直线的距离大于半径;⑤要求离心率的范围,只需用含参数a的式子表示离心率,再根据a的范围求出e的范围.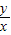 =
=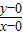 ,可看成点(x,y)与点(0,0)连线的斜率,也即圆(x-2)2+y2=3上点与坐标原点连线的斜率.
,可看成点(x,y)与点(0,0)连线的斜率,也即圆(x-2)2+y2=3上点与坐标原点连线的斜率.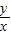 的最值即为过原点的直线与圆相切时该直线的斜率,设过原点的圆的切线方程为y=kx,即kx-y=0,
的最值即为过原点的直线与圆相切时该直线的斜率,设过原点的圆的切线方程为y=kx,即kx-y=0,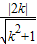 =
=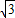 ,解得k=±
,解得k=± ,∴
,∴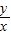 的最大值为
的最大值为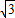 ,∴①正确.
,∴①正确.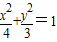 中a=2,c=1,∴离心率为
中a=2,c=1,∴离心率为 ,椭圆
,椭圆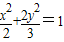 中a=
中a=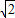 ,c=
,c=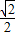 ,∴离心率为
,∴离心率为 ,∴②正确.
,∴②正确.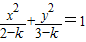 ,∴(2-k)(3-k)<0,∴2<k<3,∴2-k<0.3-k>0,∴双曲线的焦点在y轴上,
,∴(2-k)(3-k)<0,∴2<k<3,∴2-k<0.3-k>0,∴双曲线的焦点在y轴上,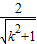 >1,解得,-
>1,解得,-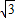 <k<
<k<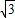 ,若-
,若-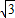 <k<
<k<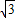 ,则圆心到直线的距离大于半径,∴圆与直线无公共点,∴圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是
,则圆心到直线的距离大于半径,∴圆与直线无公共点,∴圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是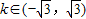 ,∴④正确.
,∴④正确.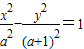 ,∴c2=a2+(a+1)2,
,∴c2=a2+(a+1)2,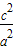 =
=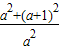 =
=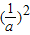 +
+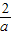 +2=
+2= +1,∵a>1,∴0<
+1,∵a>1,∴0< <1,
<1, <e<
<e<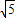 ∴⑤正确.
∴⑤正确.

 的最大值为
的最大值为 ;②椭圆
;②椭圆 与椭圆
与椭圆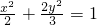 有相同的离心率;③双曲线
有相同的离心率;③双曲线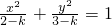 的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是
的焦点坐标是(1,0),(-1,0)④圆x2+y2=1与直线y=kx+2没有 公共点的充要条件是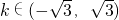 ⑤设a>1,则双曲线
⑤设a>1,则双曲线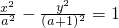 的离心率e的取值范围是
的离心率e的取值范围是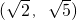 .
.