|
|
解答题:解答应写出必要的文字说明,证明过程或演算步骤.
已知各项均为正数的数列{an}前n项和为Sn,首项为a1,且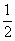 ,an,Sn成等差数列. ,an,Sn成等差数列.
| (1) |
|
(2) |
|
若an2=(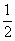 )bn,设cn= )bn,设cn=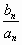 ,求数列{cn}的前n项和Tn. ,求数列{cn}的前n项和Tn.
|
|
|
答案:
解析:
(1) |
解:由题意知2an=Sn+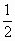 ,an>0 ,an>0
当n=1时,2a1=a1+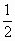 ∴a1= ∴a1=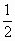
当n≥2时,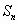 =2an- =2an-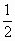 ,Sn-1=2an-1- ,Sn-1=2an-1-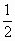
两式相减得an=2an-2an-1
整理得: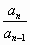 =2………………………………………………………4分 =2………………………………………………………4分
∴数列{an}是以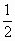 为首项,2为公比的等比数列. 为首项,2为公比的等比数列.
an=a1·2n-1=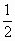 ×2n-1=2n-2………………………………………………5分 ×2n-1=2n-2………………………………………………5分
|
(2) |
解:an2= =22n-4 =22n-4
∴bn=4-2n……………………………………………………………………6分
Cn=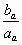 = = = =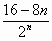
Tn=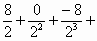 … …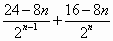 ① ①
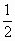 Tn= Tn=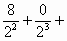 …+ …+ ② ②
①—②得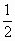 Tn=4-8 Tn=4-8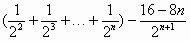 ………………………9分 ………………………9分
=4-8·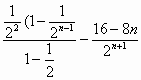
=4-4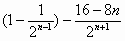
= …………………………………………………11分 …………………………………………………11分
∴Tn=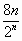 ……………………………………………………………12分 ……………………………………………………………12分
|
练习册系列答案
相关习题
科目:高中数学
来源:广东实验中学华南师附中广州市第六中学2007届高三级月考试卷(一)、数学(理工类)、(集合与逻辑、函数、导数?
题型:044
|
|
解答题:解答时应写出文字说明、证明过程或演算步骤
已知二次函数f(x)=ax2+bx+c
| (1) |
|
若任意x1,x2∈R,且x1<x2,都有f(x1)≠f(x2),求证:关于x的方程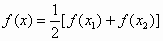 有两个不相等的实数根且必有一个根属于 有两个不相等的实数根且必有一个根属于 ; ;
|
|
(2) |
|
|
查看答案和解析>>
科目:高中数学
来源:甘肃省兰州一中2006-2007学年度第一学期高三年级期中考试、数学(理)试题
题型:044
|
|
解答题:解答应写出文字说明,证明过程或演算步骤
已知函数f(x)=x2-1(x≥1)的图像C1,曲线C2与C1关于直线y=x对称
| (1) |
|
(2) |
|
设函数y=g(x)的定义域为M,x1,x2∈M,且 ,求证: ,求证: ; ;
|
|
(3) |
|
设A,B为曲线C2上任意不同的两点,试证明直线AB与直线y=x必相交
|
|
|
查看答案和解析>>
科目:高中数学
来源:北京九中2006-2007学年度第一学期高三期中数学统练试题(理科)
题型:044
|
|
解答题:解答时应写出文字说明、证明过程或演算步骤.
已知函数f(x)的定义域为R(实数集),且对于任意实数x,y总有f(x+y)=f(x)·f(y)成立.
| (1) |
|
试说明函数y=f(x)的图象必通过(0,0)点,或通过(0,1)点;
|
|
(2) |
|
|
查看答案和解析>>
科目:高中数学
来源:绥宁二中2007届高三数学第四次月考试卷(文科)
题型:044
|
|
解答题:解答应写出文字说明、证明过程或演算步骤.
袋中装有m个红球和n个白球,m≥n≥2,这些红球和白球除了颜色不同以外,其余都相同.从袋中同时取出2个球.
| (1) |
|
若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍,试证:m必为奇数
|
|
(2) |
|
在m,n的数组中,若取出的球是同色的概率等于不同色的概率,试求m+n≤40的所有数组(m,n).
|
|
|
查看答案和解析>>


