
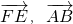 的坐标,利用向量的数量积公式求出
的坐标,利用向量的数量积公式求出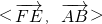 ,根据异面直线所成的角与向量角的关系求出答案.
,根据异面直线所成的角与向量角的关系求出答案. ,
,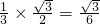 ,
,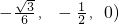 ,B(
,B(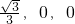 ),F(0,0,0)
),F(0,0,0)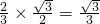 ,
,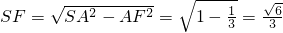 ,
,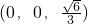 ,E(
,E(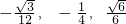 ),
),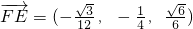 ,
,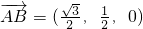 ,
,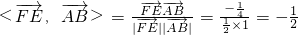
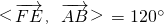 ,
,


科目:高中数学 来源:2011年广东省广州市仲元中学高三数学专题训练:直线、平面、简单几何(解析版) 题型:选择题



查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州市高三摸底考试数学卷 题型:选择题
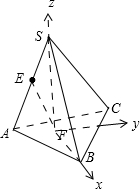
如图,在正四面体S—ABC中,E为SA的中点,F为DABC的
中心,则异面直线EF与AB所成的角是
A.30° B.45°
C.60° D.90°

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年东北师大附中四摸) 如图,在正四面体S―ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是
A.30° B.45°
C.60° D.90°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com