Question

如图，已知∠BSC＝90°，∠BSA＝∠CSA＝60°，SA＝SB＝SC，求证：平面ABC⊥平面SBC．

Answer 1

答案：
解析：

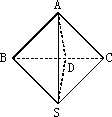
　　证明：由∠BSA＝∠CSA＝60°，及SA＝SB＝SC知，△SAB与△SAC均为等边三角形．

　　取BC的中点D，连接SD，AD．

　　因为SB＝SC，AB＝AC，所以SD⊥BC，AD⊥BC．

　　所以∠ADS为平面ABC与平面SBC所成二面角的平面角．

　　令SA＝SB＝SC＝a，由∠BSC＝90°，得BC＝a，SD＝a．

　　又由AB＝AC＝a，BC＝a，知∠BAC＝90°，则AD＝a．

　　由AD²＋SD²＝SA²，知AD⊥SD，即∠ADS＝90°．

　　故平面ABC⊥平面SBC．

　　点评：由两个平面互相垂直的定义知，若两个平面所成的二面角是直二面角，则这两个平面互相垂直．在证明两平面垂直时，可以先作二面角的平面角，再证其平面角是直角．显然，合理、准确地作出二面角的平面角是解本题的关键．