
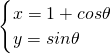 (θ为参数)上求一点,使它到直线C2:
(θ为参数)上求一点,使它到直线C2: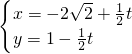 (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离. -1=0 …(2分)
-1=0 …(2分) …(5分)
…(5分) )+2|…(7分)
)+2|…(7分) =
= 时,即θ=
时,即θ= 时,d取最小值1…(9分)
时,d取最小值1…(9分) ,-
,- )…(10分)
)…(10分)

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
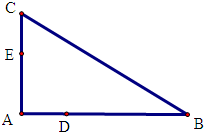 选修4-1:几何证明选讲
选修4-1:几何证明选讲查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 |
| AC |
 |
| BD |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省白山市靖宇一中高三(上)期中数学试卷(解析版) 题型:解答题
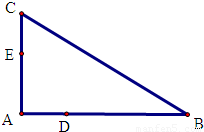
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省聊城市临清三中高三(上)期末数学考前试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com