
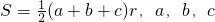 为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为
为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为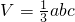
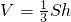
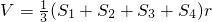 (S1,S2,S3,S4分别为四面体的四个面的面积,r为四面体内接球的半径)
(S1,S2,S3,S4分别为四面体的四个面的面积,r为四面体内接球的半径)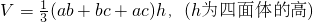
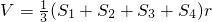 ,
,

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:2015届福建晋江季延中学高二上学期期中考试文数学试卷(解析版) 题型:解答题
知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 ,直线l的方程为:
,直线l的方程为:
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知直线l与椭圆 相交于
相交于 、
、 两点
两点
①若线段 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;
的值;
②已知点 ,求证:
,求证: 为定值
为定值
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市望子成龙学校高二(上)期中数学模拟试卷(解析版) 题型:选择题
 ,D为棱CB的中点,则该三棱锥的左视图的面积为( )
,D为棱CB的中点,则该三棱锥的左视图的面积为( )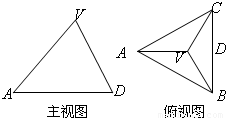

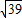
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省梅州市兴宁一中高二(下)期中数学试卷(文科)(解析版) 题型:选择题
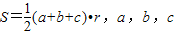 为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )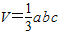
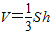
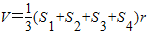 (S1,S2,S3,S4分别为四面体的四个面的面积,r为四面体内接球的半径)
(S1,S2,S3,S4分别为四面体的四个面的面积,r为四面体内接球的半径)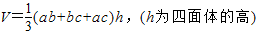
查看答案和解析>>
科目:高中数学 来源:2012年湖北省孝感高中高三5月数学练习题1(文科)(解析版) 题型:选择题
 ,D为棱CB的中点,则该三棱锥的左视图的面积为( )
,D为棱CB的中点,则该三棱锥的左视图的面积为( )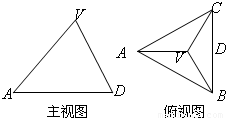
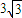
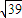
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉外国语学校、钟祥一中高三(下)4月联考数学试卷(文科)(解析版) 题型:选择题
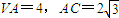 ,D为棱CB的中点,则该三棱锥的左视图的面积为( )
,D为棱CB的中点,则该三棱锥的左视图的面积为( )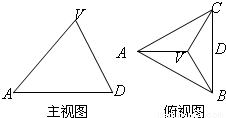
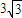
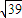
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com