
设平面内有 条直线(
条直线(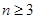 ),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用 表示这
表示这 条直线交点的个数,
条直线交点的个数,  =
=
A.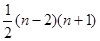 B.
B. C.
C.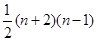 D.
D.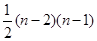
A
【解析】
试题分析:首先由图可得f(4)的值,进而逐一给出f(3),f(4),…,的值,分析可得从n-1条直线增加为n条直线时,交点的数目会增加n-1,即f(n)=f(n-1)+n-1,然后利用数列求和的办法计算可得答案. 解:如图,4条直线有5个交点,故f(4)=5,由f(3)=2,=f(4)=f(3)+3,…分析可得,从n-1条直线增加为n条直线时,交点的数目会增加n-1, f(n)=f(n-1)+n-1,累加可得f(n)=2+3+…+(n-2)+(n-1)=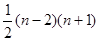
故选A.
考点:归纳推理
点评: 本题考查归纳推理的运用,注意运用数列的性质来发现其中的规律,并进行计算


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2012-2013学年广东省东莞市第七高级中学高二3月月考理科数学试卷(带解析) 题型:单选题
设平面内有 条直线(
条直线(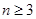 ),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用 表示这
表示这 条直线交点的个数,
条直线交点的个数,  =
=
A.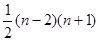 | B.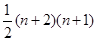 | C.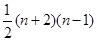 | D.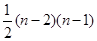 |
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
设平面内有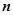
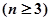 条直线,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
条直线,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用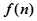 表示这
表示这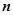 条直线交点的个数,则
条直线交点的个数,则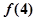 = ▲ ;当
= ▲ ;当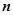 >4时,
>4时,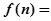 ▲ .
▲ .
|
|
|
|
|
|
4 |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二下学期第一次月考理科数学试卷 题型:填空题
设平面内有 条直线
条直线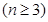 ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用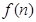 表示这
表示这 条直线交点的个数,则
条直线交点的个数,则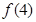 =______;当
=______;当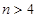 时,
时,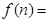 _____________________.(用
_____________________.(用 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
(05年广东卷)设平面内有![]() 条直线
条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这
表示这![]() 条直线交点的个数,则
条直线交点的个数,则![]() =____________;当
=____________;当![]() 时,
时,![]() .(用
.(用![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com