某学校4名男学生在旅行社组织下外出旅游,现旅行社有6个房间可以安排住宿,每人可以进住任何一个房间,且进住各房间是等可能的,试求(注:计算结果化成最简分数)
(1)指定的4个房间中各有1人的概率?
(2)恰有4个房间中各有1人的概率?
(3)指定的某个房间中有2人的概率?
解:(1)所有的住宿方法有6
4种,指定的4个房间中各有1人的住宿方法有A
44种,
故指定的4个房间中各有1人的概率
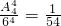
.(4分)
(2)恰有4个房间中各有1人的住宿方法有 C
64A
44 种,
故恰有4个房间中各有1人的概率为
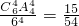
=

.(4分)
(3)从4个人中任意选出2个人,放到某个房间中有C
42种不同的方法,
其余的2个人任意住到剩余的5个房间内,有5
2种,故指定的某个房间中有2人的宿方法有 C
42•5
2 种方法,
故指定的某个房间中有2人的概率
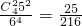
.(5分)
分析:(1)所有的住宿方法有6
4种,指定的4个房间中各有1人的住宿方法有A
44种,由此求得指定的4个房间中各有1人的概率.
(2)恰有4个房间中各有1人的住宿方法有 C
64A
44 种,从而求得恰有4个房间中各有1人的概率.
(3)从4个人中任意选出2个人,放到某个房间中有C
42种不同的方法,其余的2个人任意住到剩余的5个房间内,
有5
2种方法,故指定的某个房间中有2人的宿方法有 C
42•5
2 种,由此求得指定的某个房间中有2人的概率.
点评:本题主要考查等可能事件的概率,求出满足条件的住宿方法,是解题的关键.

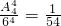 .(4分)
.(4分)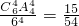 =
= .(4分)
.(4分)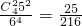 .(5分)
.(5分)
