Question

设A、B分别为椭圆=1(a,b＞0)的左、右顶点，椭圆长半轴的长等于焦距，且x=4为它的右准线.

（1）求椭圆的方程；

（2）设P为右准线上不同于点（4，0）的任意一点，若直线AP、BP分别与椭圆相交于异于A、B的点M、N，证明点B在以MN为直径的圆内.

Answer 1

解：（1）依题意得 a＝2c，=4，解得a=2，c=1，从而b=.

故椭圆的方程为=1.

（2）解法1：由（1）得A（-2，0），B（2，0）.设M（x₀，y₀）.

∵M点在椭圆上，∴y₀=（4-x₀²）.①又点M异于顶点A、B，∴-2＜x₀＜2，

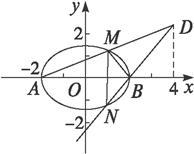
由P、A、M三点共线可以得P（4，）.

从而=（x₀-2，y₀），=（2，）.

∴·=2x₀-4++2=（x₀²-4+3y₀²）②

将①代入②，化简得·=（2-x₀）.

∵2-x₀＞0，∴·＞0，则∠MBP为锐角，从而∠MBN为钝角，

故点B在以MN为直径的圆内.

解法2：由（1）得A（－2，0），B（2，0）.

设M（x₁，y₁），N（x₂，y₂），则－2＜x₁＜2，－2＜x₂＜2，又MN的中点Q的坐标为（）.依题意，计算点B到圆心Q的距离与半径的差

|BQ|²-|MN|²=(-2)²+()²-[(x₁－x₂)²＋(y₁－y₂)²]=（x₁-2）(x₂-2)＋y₁y₂ ③

又直线AP的方程为y=(x+2)，直线BP的方程为y=(x-2).

而两直线AP与BP的交点P在准线x＝4上，

∴，即y₂=.                   ④

又点M在椭圆上，则=1，即y₁²=(4-x₁²).   ⑤

于是将④⑤代入③，

化简后可得|BQ|²-|MN|²=（2-x₁）(x₂-2)＜0.

从而，点B在以MN为直径的圆内.