
 如图所示,圆柱底面的直径AB长度为2
如图所示,圆柱底面的直径AB长度为2 ,O为底面圆心,正三角形ABP的一个顶点P在上底面的圆周上,PC为圆柱的母线,CO的延长线交⊙O于点E,BP的中点为F.
,O为底面圆心,正三角形ABP的一个顶点P在上底面的圆周上,PC为圆柱的母线,CO的延长线交⊙O于点E,BP的中点为F. ,∴Rt△PAC≌Rt△PBC,
,∴Rt△PAC≌Rt△PBC, 则C(0,0,0),F(0,1,1),O(1,1,0),P(0,0,2)…(9分)
则C(0,0,0),F(0,1,1),O(1,1,0),P(0,0,2)…(9分)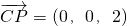 为平面CEB的一个法向量…(10分)
为平面CEB的一个法向量…(10分) 平面CEF的一个法向量,∵
平面CEF的一个法向量,∵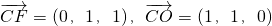
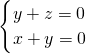 ,令y=-1,则
,令y=-1,则 …(11分)
…(11分)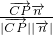 =
= …(12分)
…(12分) ,…(13分)
,…(13分) =
= …(14分)
…(14分)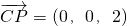 为平面CEB的一个法向量,平面CEF的一个法向量为
为平面CEB的一个法向量,平面CEF的一个法向量为 ,利用向量的夹角公式,即可求得二面角F-CE-B的正切值.
,利用向量的夹角公式,即可求得二面角F-CE-B的正切值.

科目:高中数学 来源: 题型:
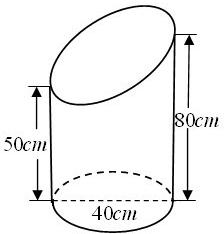
| A、2600cm2 | B、5200cm2 | C、2600πcm2 | D、5200πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•茂名二模)如图所示,圆柱底面的直径AB长度为2
(2012•茂名二模)如图所示,圆柱底面的直径AB长度为2| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省茂名市高三下学期第二次高考模拟考试理科数学试卷(解析版) 题型:解答题
如图所示,圆柱底面的直径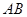 长度为
长度为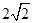 ,
,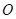 为底面圆心,正三角形
为底面圆心,正三角形 的一个顶点
的一个顶点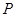 在上底面的圆周上,
在上底面的圆周上,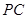 为圆柱的母线,
为圆柱的母线,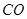 的延长线交
的延长线交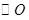 于点
于点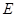 ,
, 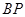 的中点为
的中点为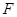 .
.
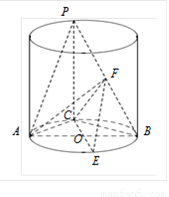
(1)
求证:平面 ⊥平面
⊥平面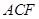 ;
;
(2)
求二面角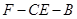 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com