
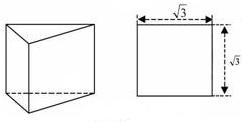
 如图,一个正三棱柱的左(侧)视图是边长为
如图,一个正三棱柱的左(侧)视图是边长为 的正方形,则它的外接球的表面积等于
的正方形,则它的外接球的表面积等于 π
π π
π ,底面正三角的高也是
,底面正三角的高也是 .设球心为O,半径为R,△ABC的中心为G,所以△OGA是直角三角形,OG是高的一半,OG=
.设球心为O,半径为R,△ABC的中心为G,所以△OGA是直角三角形,OG是高的一半,OG= ,所以GA=
,所以GA= .在△OAG中由勾股定理得:R2=
.在△OAG中由勾股定理得:R2= .进而得到答案.
.进而得到答案. 的正方形,
的正方形, ,底面正三角的高也是
,底面正三角的高也是 .
. ,
, ,
, .
. .
.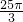 .
.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com