
求抛物线y=2x2与直线x=0,x=1,y=0所围成的平面图形的面积S.
|
解:(1)分割 在区间[0,1]上等间隔地插入n-1个点,将它等分成n个小区间:[0, 记第i个区间为[ S= (2)近似代替 记f(x)=2x2,当n很大,即Δx很小时,在区间[ ΔSi≈Δ =2( (3)求和 小曲边梯形的面积和Sn≈ 从而得到S的近似值, S=Sn= (4)取极限 分别将区间[0,1]等分成8,16,20,…等份时,可以看到随着n的不断增大,即Δx越来越小时,Sn= |


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:学习周报 数学 人教课标版高二(A选修2-1) 2009-2010学年 第19期 总第175期 人教课标版(A选修2-1) 题型:044
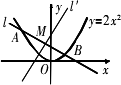
直线l与抛物线y=2x2交于A,B两点,![]() 是AB的垂直平分线,当
是AB的垂直平分线,当![]() 的斜率为2时,求
的斜率为2时,求![]() 在y轴上截距的取值范围.
在y轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试(陕西卷)、数学(文科) 题型:044
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线交C于点N.
(Ⅰ)证明:抛物线C在点N处的切线与AB平行;
(Ⅱ)是否存在实数k使![]() ,若存在,求k的值;若不存在,说明理由.
,若存在,求k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:福建省厦门市翔安一中2012届高三11月月考数学理科试题 题型:044
已知A(-1,2)为抛物线C:y=2x2上的点.直线l1过点A,且与抛物线C相切.直线l2:x=a(a≠1)交抛物线C于点B,交直线l1于点D.

(1)求直线l1的方程;
(2)设△ABD的面积为S1,求|BD|及S1的值;
(3)设由抛物线C、直线l1、l2所围成的图形的面积为S2,求证:S1∶S2的值为与a无关的常数.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考文科数学 题型:解答题
(本小题满分13分)
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴
的垂线交C于点N.(1)证明:抛物线C在点N处的切线与AB平行;
(2)是否存在实数k使·=0,若存在,求k的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com