
设函数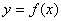 是定义在
是定义在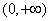 上的减函数,并且满足
上的减函数,并且满足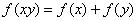 ,
,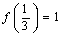
(1)求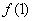 ,
,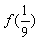 ,
,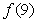 的值,(2)如果
的值,(2)如果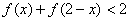 ,求x的取值范围。
,求x的取值范围。
解:(1)令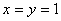 ,则
,则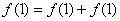 ,∴
,∴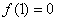 ……1分
……1分
令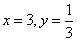 , 则
, 则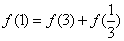 , ∴
, ∴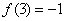 ………2分
………2分
∴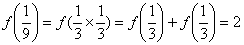 …………4分
…………4分
∴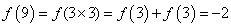 …………… 6分
…………… 6分
(2)∵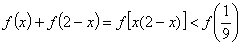 ,
,
又由 是定义在R+上的减函数,得:
是定义在R+上的减函数,得:
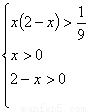 ……… 8分
……… 8分
解之得: ………… 12分
………… 12分
【解析】本试题主要是考查了抽象函数的赋值思想的运用,以及运用单调性求解不等式的综合运用。
(1)令x=y=1,k可知结论f(1)=0,令x=3,y= 得到结论。
得到结论。
(2)将所求的不等式合并,借助于单调性得到x的范围。


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2014届广东始兴县风度中学高一数学竞赛试卷(解析版) 题型:解答题
(本小题满分14分)
设函数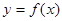 是定义在
是定义在 上的减函数,并且满足
上的减函数,并且满足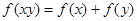 ,
,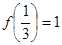 ,
,
(1)求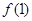 的值,
(2)如果
的值,
(2)如果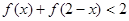 ,求x的取值范围。(16分)
,求x的取值范围。(16分)
查看答案和解析>>
科目:高中数学 来源:2010年河南省周口市高一上学期期中考试数学卷 题型:解答题
(本题满分12分)设函数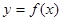 是定义在
是定义在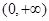 上的减函数,并且满足
上的减函数,并且满足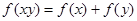 ,
,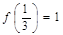 ,
,
(1)求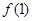 ,
,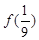 ,
,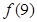 的值,
(2)如果
的值,
(2)如果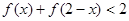 ,求x的取值范围。
,求x的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010年江西省四校联考高一上学期期中考试数学试卷 题型:解答题
(本题满分12分)设函数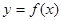 是定义在
是定义在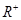 上的减函数,并且满足
上的减函数,并且满足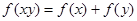 ,
,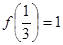 ,
,
(1)求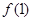 的值,
(2)如果
的值,
(2)如果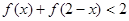 ,求x的取值范围。
,求x的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com