练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图1， 中， ，点为线段的四等分点，线段互相平行，现沿折叠得到图2所示的几何体，此几何体的底面为正方形.

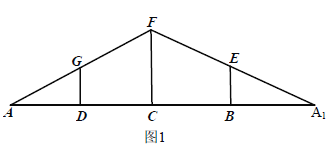
    （1）证明： 四点共面；（2）求四棱锥的体积.

    【答案】（1）见解析；（2）.

    【解析】试题分析：（1）取FC中点M,连接EM,DM,易得EM||BC，可得四边形AEMD为平行四边形，进而可证得四点共面；

    （2）利用即可求体积.

    试题解析：

    由题得FC⊥，DG=BE=1，所以在图2中FC⊥, FC⊥, ,所以, 又BE,CF,DG互相平行，则BE,CF,DG均与底面垂直

    （1）利用即可求得.

    取FC中点M,连接EM,DM,易得EM||BC,且EM=BC，AD||BC,且AD=BC，

    所以四边形AEMD为平行四边形，所以AE||DM,易得GF||DM,则AE||GF,

    所以A,E,F,G四点共面

    (2)

    如图，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥中，PA⊥平面ABCD，底面ABCD是边长为a的菱形，∠BAD=120°，PA=b．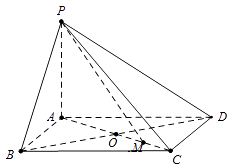

    （1）求证：平面PBD⊥平面PAC；
    （2）设AC与BD交于点O，M为OC中点，若二面角O﹣PM﹣D的正切值为2 ，求a：b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=x+ 有如下性质：如果常数t＞0，那么该函数在 上是减函数，在 上是增函数．
    （1）已知f（x）= ，x∈[﹣1，1]，利用上述性质，求函数f（x）的单调区间和值域；
    （2）对于（1）中的函数f（x）和函数g（x）=﹣x﹣2a，若对任意x1∈[﹣1，1]，总存在x2∈[0，1]，使得g（x2）=f（x1）成立，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知幂函数f（x）=xa的图象经过点（ ， ）．
    （1）求函数f（x）的解析式，并判断奇偶性；
    （2）判断函数f（x）在（﹣∞，0）上的单调性，并用单调性定义证明．
    （3）作出函数f（x）在定义域内的大致图象（不必写出作图过程）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义域为R的偶函数，当x≥0时，f（x）=x2﹣4x，那么当x＜0时，f（x）= ， 不等式f（x+2）＜5的解集是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy 中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），离心率e=．

    （1）求椭圆G 的标准方程；

    （2）已知直线l1：y=kx+m1与椭圆G交于 A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|=|CD|，如图所示．

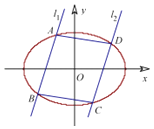
    ①证明：m1+m2=0；

    ②求四边形ABCD 的面积S 的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列三个命题
    ①若“p或q”为假命题，则p，q均为真命题；
    ②命题“若x≥2且y≥3，则x+y≥5”的逆否命题为假命题；
    ③在△ABC中，“A＞45°”是“sinA＞ ”的充要条件，
    其中正确的命题个数是（ ）
    A.3
    B.2
    C.1
    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知全集U={1，2，3，4}，集合A={1，2，x2}与B={1，4}是它的子集，
    （1）求UB；
    （2）若A∩B=B，求x的值；
    （3）若A∪B=U，求x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是定义在R上不恒为0的函数，且对于任意的实数a，b满足f（2）=2，f（ab）=af（b）+bf（a），an= （n∈N*），bn= （n∈N*），给出下列命题：
    ①f（0）=f（1）；
    ②f（x）为奇函数；
    ③数列{an}为等差数列；
    ④数列{bn}为等比数列．
    其中正确的命题是 ． （写出所有正确命题的序号）

    查看答案和解析>>

    同步练习册答案