
已知偶函数y=f(x)=ax2+bx+c的最小值为-1,且f(1)=0.
(1)求该函数的表达式f(x).
(2)过曲线C:y=f(x)(x>0)上的点P作曲线C的切线,与x轴、y轴分别交于点M,N,试确定点P的坐标,使△MON的面积最小.
[求商的导数的法则是: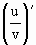 =
=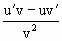 ]
]
|
解:(1)因为该函数为偶函数, 所以f(-x)=f(x)对定义域内一切x∈R正成立.所以f(-1)=f(1),所以b=0.因为f(1)=0,所以a+c=0,c=-a.所以f(x)=ax2-a.由此,当a>0时,f(x)有最小值-a.所以-a=-1,a=1,所以f(x)=x2-1. (2)如图所示,设切点为P(u,t),则t=u2-1.因为y=x2-1(x>0),所以
所以过P点的切线l的方程为y-t=2u(x-u).则切线l与x,y轴的交点分别为M( |


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数y=Asin(ωx+![]() )(A>0,ω>0)的图象过点P(
)(A>0,ω>0)的图象过点P(![]() ,0),图象上与点P最近的一个顶点是Q(
,0),图象上与点P最近的一个顶点是Q(![]() ,5).
,5).
(1)求函数的解析式;
(2)指出函数的增区间;
(3)求使y≤0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知抛物线y=x2-2x-8.
(1)求抛物线顶点的坐标;
(2)求将这条抛物线顶点平移到点(2,-3)时的函数解析式;
(3)将这条抛物线按a=(h,k)平移,使平移后的抛物线的解析式恰为y=x2,求h,k.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知函数y=-2x2-12x-20按a平移后,顶点在x=2上,且x轴上截得的弦长为b.求a及平移后的解析式.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知直线y=-kx-2,P(-2,1),Q(3,2).
(1)当k=-2时,这条直线与直线PQ的交点分PQ所成的比是多少?
(2)当这条直线和线段PQ有交点时,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com