
 已知方向向量为v=(1,
已知方向向量为v=(1, )的直线l过点(0,-2
)的直线l过点(0,-2 )和椭圆C:
)和椭圆C: +
+ =1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
=1(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上. •
• =
= .cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
.cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由. x-2
x-2 ,过原点垂直l的直线方程为y=-
,过原点垂直l的直线方程为y=- x,这两个方程联立可知x=
x,这两个方程联立可知x= .再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知
.再由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,可知 =3.由此可以求出椭圆C的方程.
=3.由此可以求出椭圆C的方程. x-3
x-3 .设原点关于直线l对称点为(p,q),则
.设原点关于直线l对称点为(p,q),则 解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知
解得p=3.由椭圆中心(0,0)关于直线l的对称点在椭圆C的右准线上,知 =3.由此能够推出椭圆C的方程.
=3.由此能够推出椭圆C的方程. +
+ =1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解.
=1,整理得(3k2+1)x2+12k2x+12k2-6=0,再由根与系数的关系和点到直线 的距离求解. x-2
x-2 ,①
,① x,②
x,② .
. =2×
=2× =3.
=3. +
+ =1③
=1③ x-3
x-3 .
. 解得p=3.
解得p=3. =3.
=3. +
+ =1③
=1③ (II)解:设M(x1,y1),N(x2,y2).
(II)解:设M(x1,y1),N(x2,y2). ,x1•x2=
,x1•x2= ,
, =
= =
= ,
,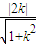 .
. •
• =
= cot∠MON,即|
cot∠MON,即| |•|
|•| |cos∠MON=
|cos∠MON= ≠0,
≠0, |•|
|•|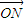 |sin∠MON=4
|sin∠MON=4 ,∴S△OMN=
,∴S△OMN= .∴|MN|•d=
.∴|MN|•d= ,
, |k|
|k| =
= (3k2+1),
(3k2+1), ,∴k=±
,∴k=± .
. 当直线m垂直x轴时,也满足S△OMN=
当直线m垂直x轴时,也满足S△OMN=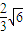 .
. x+
x+ ,或y=-
,或y=-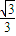 x-
x- ,或x=-2.
,或x=-2. •
• ≠0.
≠0. x+
x+ ,或y=-
,或y=- x-
x- ,或x=-2.
,或x=-2.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
| v |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| DM |
| DN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知方向向量为v=(1,
已知方向向量为v=(1,| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| OM |
| ON |
| 4 |
| 3 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| v |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| v |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| V |
| 3 |
| x2 |
| a 2 |
| y2 |
| b2 |
| 3 |
| 6 |
| OM |
| ON |
4
| ||
| 3tan∠MON |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com