练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若关于的方程=3+a有实数根，则实数的取值范围是            .


     a>-3   

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图是一个空间几何体的三视图，则该几何体的侧面积为（   ）

    A．                 B．    C．        D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A=｛2，5，6｝，B=｛3，5｝，则集合A∪B=           ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：方程x2＋mx＋1＝0有负实数根；
    命题q：方程4x2＋4(m－2)x＋1＝0无实数根，
    若“p或q”为真命题，“p且q”为假命题，求实数m的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若A=+i，则A2=            .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：∀x∈[1,12]，x2－a≥0.命题q：∃x0∈R，使得x＋(a－1)x0＋1<0.若p或q为真，p且q为假，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数的虚部为               

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合是满足下列性质函数的的全体，在定义域内存在，使得成立。（1）函数，是否属于集合？分别说明理由。（2）若函数属于集合，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     甲、乙两地相距s千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时。已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度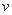（千米/时）的平方成正比，比例系数为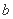；固定部分为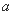元．

    （1）把全程运输成本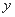(元)表示为速度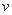（千米/时）的函数，并指出这个函数的定义域；

    （2）为了使全程运输成本最小，汽车应以多大速度行驶？

    查看答案和解析>>

    同步练习册答案