不等式（x+1）（2-x）＞0的解集为（ ）
A．{x|x＜-1或x＞1}
B．{x|x＜-2或x＞1}
C．{x|-2＜x＜1}
D．{x|-1＜x＜2}
【答案】
分析：在不等式两边同时乘以-1，不等号方向改变，把2-x变为x-2，根据两数相乘，异号得负可把原不等式化为两个不等式组，分别求出不等式组的解集，即可得到原不等式的解集．
解答：解：不等式（x+1）（2-x）＞0，
即（x+1）（x-2）＜0，
可化为：
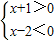
或
，
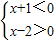
解得：-1＜x＜2，
则原不等式的解集为{x|-1＜x＜2}．
故选D
点评：此题考查了一元二次不等式不等式的解法，利用了转化的数学思想，是高考中常考的基本题型．一元二次不等式转化为不等式组的理论依据为：两数相乘同号得正、异号得负的取符号法则．
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
