
分析 Sn-Sn-2=3×(-$\frac{1}{2}$)n-1(n≥3),对n分类讨论,利用等比数列的求和公式即可得出.
解答 解:∵Sn-Sn-2=3×(-$\frac{1}{2}$)n-1(n≥3),
∴考虑偶数2n时,S2n-S2n-2=3×$(-\frac{1}{2})^{2n-1}$,
∴S2n=(S2n-S2n-2)+(S2n-2-S2n-4)+…+(S4-S2)+S2
=S2-3$[(\frac{1}{2})^{2n-1}$+$(\frac{1}{2})^{2n-3}$+…+$(\frac{1}{2})^{3}]$
=-3×$\frac{\frac{1}{2}[1-\frac{1}{{4}^{n}}]}{1-\frac{1}{4}}$=-2$(1-\frac{1}{{4}^{n}})$=-2+$(\frac{1}{2})^{2n-1}$.
同理可得:奇数项S2n+1-S2n-1=3×$(-\frac{1}{2})^{2n}$=3×$(\frac{1}{2})^{2n}$.
∴S2n+1=(S2n+1-S2n-1)+(S2n-1-S2n-3)+…+(S3-S1)+S1
=1+3$[(\frac{1}{2})^{2n}+$$(\frac{1}{2})^{2n-2}$+…+$(\frac{1}{2})^{2}]$
=1+3×$\frac{\frac{1}{4}[1-(\frac{1}{4})^{n}]}{1-\frac{1}{4}}$=2-$(\frac{1}{2})^{2n}$.
∴a2n+1=S2n+1-S2n=2-$(\frac{1}{2})^{2n}$-$[-2+(\frac{1}{2})^{2n-1}]$=4-3×$(\frac{1}{2})^{2n}$.
a2n=S2n-S2n-1=-2+$(\frac{1}{2})^{2n-1}$-$[2-(\frac{1}{2})^{2n-2}]$=-4+3×$(\frac{1}{2})^{2n-1}$.
a1=S1=1.
综上可得:an=$\left\{\begin{array}{l}{4-3×(\frac{1}{2})^{n-1},n为奇数}\\{-4+3×(\frac{1}{2})^{n-1},n为偶数}\end{array}\right.$.
故答案为:an=$\left\{\begin{array}{l}{4-3×(\frac{1}{2})^{n-1},n为奇数}\\{-4+3×(\frac{1}{2})^{n-1},n为偶数}\end{array}\right.$.
点评 本题考查了等比数列的通项公式与求和公式、递推关系,考查了分类讨论方法、推理能力与计算能力,属于难题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,DF⊥AB于点F,且AE=8,AB=10.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,DF⊥AB于点F,且AE=8,AB=10.| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
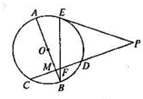 如图所示,AB是圆O的直径,PC是圆O的一条割线,且交圆O于C、D两点,AB⊥PC,PE是圆O的一条切线,切点为E,AB与BE分别交PC于M、F两点.
如图所示,AB是圆O的直径,PC是圆O的一条割线,且交圆O于C、D两点,AB⊥PC,PE是圆O的一条切线,切点为E,AB与BE分别交PC于M、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com