Question

一个抛物线型的拱桥，当水面离拱顶2m时，水面宽4m．若水面下降1m，求水面的宽度．

Answer 1

【答案】分析：先以拱顶为原点，建立直角坐标系，再用待定系数法求抛物线的标准方程，最后将水面下降1m，求水面的宽度问题转化为y=-3时，求2x的值，利用抛物线标准方程易得此值
解答：解：如图建立直角坐标系，设抛物线的方程为x²=-2py，
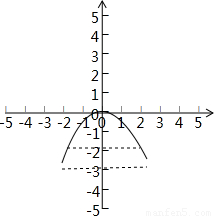
∵水面离拱顶2m时，水面宽4m
∴点（2，-2）在抛物线上，所以p=1，x²=-2y，
∵水面下降1m，即y=-3
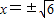
而y=-3时，所以水面宽为．
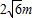
∴若水面下降1m，水面的宽度为
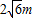点评：本题考察了解析法解决几何问题的一般方法，抛物线的标准方程及应用，熟练的将实际问题转化为数学问题是解决本题的关键