
如下图,
PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.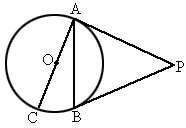
科目:高中数学 来源:云南省昆明一中2011-2012学年高一下学期期中考试数学试题 题型:022
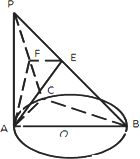
如下图,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥面PBC.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:东北育才学校2008-2009学年度高三模拟试题(理科数学) 2009.5.20 题型:044
如下图,PA、PB切⊙O于A、B两点,PO交劣弧AB于点C.
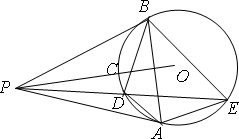
(Ⅰ)求证:点C是ΔPAB的内心;
(Ⅱ)PDE为⊙O的割线,求证:AE·DB=DA·BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)证明:PA⊥平面ABCD;
(2)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求Q点的轨迹方程;
(2)设(1)中所求轨迹为C2,C1、C2的离心率分别为e1、e2,当e1≥![]() 时,求e2的取值范围.
时,求e2的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com