
已知点M(k,l)、P(m,n),(klmn≠0)是曲线C上的两点,点M、N关于x轴对称,直线MP、NP分别交x轴于点E(xE,0)和点f(xF,0),
(Ⅰ)用k、l、m、n分别表示xE和xF;
(Ⅱ)某同学发现,当曲线C的方程为:x2+y2=R2(R>0)时,xE·xF=R2是一个定值与点M、N、P的位置无关;请你试探究当曲线C的方程为:![]() (a>b>0)时,xE·xF的值是否也与点M、N、P的位置无关;
(a>b>0)时,xE·xF的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为y2=2px(p>0)时,探究xE与xF经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| |AQ| |
| |QB| |
| |OA| |
| |OB| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| OP |
| OQ |
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MQ |
| PQ |
| HA |
| HB |
| FD |
| FB |
查看答案和解析>>
科目:高中数学 来源:福建省模拟题 题型:解答题
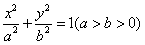 时,探究xE·xF的值是否与点M、N、P的位置相关;
时,探究xE·xF的值是否与点M、N、P的位置相关;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com