
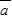 =(5
=(5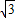 cosx,cosx),
cosx,cosx),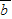 =(sinx,2cosx)其中x∈[
=(sinx,2cosx)其中x∈[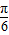 ,
,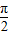 ],设函数f(x)=
],设函数f(x)=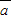 •
•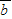 +|
+| |2+
|2+
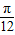 )的值.
)的值. =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)设函数f(x)=
=(sinx,2cosx)设函数f(x)= •
• +|
+| |2+
|2+ ,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[
,根据平面向量的数量积公式,我们易求出函数f(x)的解析式,进而根据二倍角公式和辅助角公式,可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数的图象和性质及其中x∈[ ,
, ],求出函数f(x)的值域;
],求出函数f(x)的值域; 的正弦值,进而根据2x+
的正弦值,进而根据2x+ 的范围求出其余弦值,进而根据f(x-
的范围求出其余弦值,进而根据f(x- )=5sin2x+5=5sin(2x+
)=5sin2x+5=5sin(2x+ -
- )+5结合两角差的正弦公式得到答案.
)+5结合两角差的正弦公式得到答案. =(5
=(5 cosx,cosx),
cosx,cosx), =(sinx,2cosx)
=(sinx,2cosx) •
• +|
+| |2+
|2+ =5
=5 cosx•sinx+2cosx•cosx+sin2x+4cos2x+
cosx•sinx+2cosx•cosx+sin2x+4cos2x+ …(2分)
…(2分) cosx•sinx+5cos2x+
cosx•sinx+5cos2x+
 sin2x+
sin2x+ cos2x+5
cos2x+5 )+5 …(5分)
)+5 …(5分) ,
, ],
], ≤2x+
≤2x+ ≤
≤ ,
, ≤sin(2x+
≤sin(2x+ )≤1…(7分)
)≤1…(7分) ,
, ]时,函数f(x)的值域为[
]时,函数f(x)的值域为[ ,10]…(8分)
,10]…(8分) )+5=8
)+5=8 )=
)= ,…(9分)
,…(9分) ≤2x+
≤2x+ ≤
≤ ,
, )=-
)=- …(11分)
…(11分) )=5sin2x+5
)=5sin2x+5 -
- )+5
)+5 )cos
)cos -cos(2x+
-cos(2x+ )sin
)sin ]+5
]+5 •
• +
+ •
• )+5
)+5 +7 …(14分)
+7 …(14分)

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| f(x1)f(x2) |
查看答案和解析>>
科目:高中数学 来源:2007-2008学年浙江省杭州师大附中高三第三次月考数学试卷(理科)(解析版) 题型:解答题
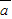 =(5
=(5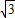 cosx,cosx),
cosx,cosx),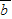 =(sinx,2cosx)其中x∈[
=(sinx,2cosx)其中x∈[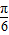 ,
,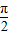 ],设函数f(x)=
],设函数f(x)=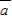 •
•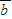 +|
+|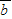 |2+
|2+
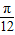 )的值.
)的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省连云港市东海高级中学高三(上)期中数学试卷(理科)(解析版) 题型:解答题
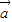 =(5
=(5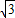 cosx,cosx),
cosx,cosx),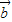 =(sinx,2cosx),函数f(x)=
=(sinx,2cosx),函数f(x)=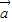
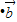 +
+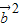 .
.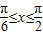 时,求函数f(x)的值域.
时,求函数f(x)的值域.查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() =(5
=(5![]() cosx,cosx),
cosx,cosx),![]() =(sinx,2cosx),设函数f(x)=
=(sinx,2cosx),设函数f(x)=![]() ·
·![]() +|
+|![]() |2+
|2+![]() .
.
(Ⅰ)当x∈[![]() ,
,![]() ],求函数f(x)的值域;
],求函数f(x)的值域;
(Ⅱ)当x∈[![]() ,
,![]() ]时,若f(x)=8,求函数f(x-
]时,若f(x)=8,求函数f(x-![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com