
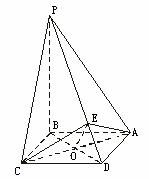
(Ⅰ)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(Ⅱ)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.
(19)本小题考查线面关系和二面角的概念,以及空间想象能力和逻辑推理能力.
(Ⅰ)解:∵PB⊥面ABCD,

∴BA是PA在面ABCD上的射影.
又DA⊥AB,
∴PA⊥DA,
∴∠PAB是面PAD与面ABCD所成的二面角的平面角,∠PAB=60°.而PB是四棱锥P—ABCD的高,
PB=AB·tan60°=![]() a,
a,
∴V锥=![]() a·a2=
a·a2=![]() a3.
a3.
(Ⅱ)证:不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP,垂足为E,连结EC,则△ADE≌△CDE,
∴AE=CE,∠CED=90°,故∠CEA是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O,连结EO,则EO⊥AC,
∴![]() a=OA<AE<AD=a.
a=OA<AE<AD=a.
在△AEC中,cosAEC=![]()
=![]() <0.
<0.
所以,面PAD与面PCD所成的二面角恒大于90°.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
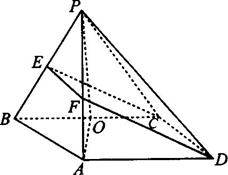
(1)求异面直线BC与PA所成的角;
(2)求二面角P-EC-D的大小;
(3)求点A到截面EFDC的距离.
第19题图
查看答案和解析>>
科目:高中数学 来源: 题型:
(福建卷文19)如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(福建卷文19)如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(重庆卷)解析版(理) 题型:解答题
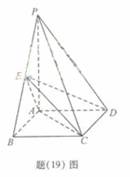 如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,
PA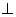 底面ABCD,PA=AB=
底面ABCD,PA=AB=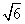 ,点E是棱PB的中点。
,点E是棱PB的中点。
(Ⅰ)求直线AD与平面PBC的距离;
(Ⅱ)若AD=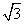 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com