【答案】
分析:(1)设出切点坐标,求出曲线在切点处的导数,运用点斜式写出切线方程,把点(1,1)代入切线方程求解切点的横坐标,然后再把求得的切点横坐标代回切线方程即可;
(2)把曲线C
2:y=x
3-3x
2+3x变形为y=(x-1)
3+1,则直观看出该函数图象是把曲线
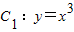
经过如何变化得到的.
解答:解:(1)设切点为P(
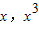
),则
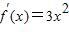
,
所以,过点P的切线方程为:
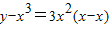
,
因为切线过点(1,1),所以有
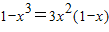
,
整理得:
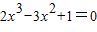
,即
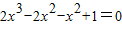
,所以,

,
也就是
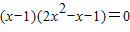
,解得:x
=1或
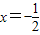
.
所以,当(1,1)为切点时,过点(1,1)的切线方程为:y-1=3(x-1),即y=3x-2.
当(1,1)不是切点时,过点(1,1)的切线方程为:
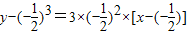
,即
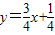
.
(2)由y=x
3-3x
2+3x=x
3-3x
2+3x-1+1=(x-1)
3+1.
所以y=x
3-3x
2+3x是把y=x
3向右平移一个单位,再向上平移一个单位得到的.
即曲线C
1向右平移一个单位,再向上平移一个单位得到曲线C
2.
点评:本题考查学生会利用导数求曲线上过某点切线方程的斜率,解答该题时一定要区分是求的曲线在某点处的切线方程还是过某点的切线方程,若是求的曲线在某点处的切线方程,则该点为切点,切线方程唯一,若求的是过某点的切线方程,则该点不见得是切点,需要设切点坐标.此题是好题,也是易错题,属中档题.

 ,曲线C2:y=x3-3x2+3x
,曲线C2:y=x3-3x2+3x 过点(1,1)的切线方程;
过点(1,1)的切线方程;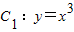 经过如何变化得到的.
经过如何变化得到的.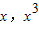 ),则
),则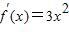 ,
,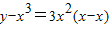 ,
,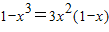 ,
,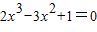 ,即
,即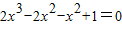 ,所以,
,所以, ,
,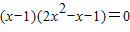 ,解得:x=1或
,解得:x=1或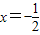 .
.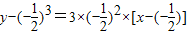 ,即
,即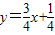 .
.
