练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

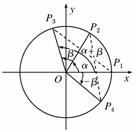
    已知＝(cosα，sinα)，＝(cosβ，sinβ)，且与之间满足关系：，其中k＞0．

    (Ⅰ)用k表示·；

    (Ⅱ)求·的最小值，并求此时与夹角的大小．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：江西省浮梁一中2007届高三数学重组卷一(人教版) 题型：044

    已知△ABC的面积S满足3≤S≤3，且·＝6，与的夹角为α

    (1)求α的取值范围

    (2)若函数f(α)＝sin2α＋2sinαcosα＋3cos2α，求f(α)的最小值．

    查看答案和解析>>

    科目：高中数学 来源：如皋中学2007－2008学年度第一学期阶段考试高三数学(理科)试卷 题型：044

    已知△ABC的面积S满足3≤S≤3且的夹角为α，

    (Ⅰ)求α的取值范围；

    (Ⅱ)求f(α)＝sin2α＋2sinαcosα＋3cos2α的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、理科数学(四川卷) 题型：044

    (Ⅰ)①证明两角和的余弦公式Cα+β：cos(α＋β)＝cosαcosβ－sinαsinβ；

    ②由Sα+β推导两角和的正弦公式Sα+β：sin(α＋β)＝sinαcosβ－cosαsinβ．

    (Ⅱ)已知△ABC的面积S＝＝3，且cosB＝，求cosC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1)①证明：两角和的余弦公式C(α＋β)：cos(α＋β)＝cos αcos β－      sin αsin β；

    ②由C(α＋β)推导两角和的正弦公式S(α＋β)：sin(α＋β)＝sin αcos β＋cos αsinβ.

    (2)已知△ABC的面积S＝，·＝3，且cos B＝，求cos C.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△ABC的面积S满足3≤S≤3，且·＝6，与的夹角为θ.

    (1)求θ的取值范围；

    (2)求函数f(θ)＝sin2θ＋2sinθcosθ＋3cos2θ的最大值.

    查看答案和解析>>

    同步练习册答案