练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某航空公司经营这四个城市之间的客运业务，它们之间的直线距离的部分机票价格如下：为2000元；为1600元；为2500元；为900元；为1200元，若这家公司规定的机票价格与往返城市间的直线距离成正比，则间直线距离的票价为（设这四个城在同一水平面上）                          （   ）
    A．1500元B．1400元C．1200元D．1000元
    A
    分析：这家公司所规定的机票价格与往返城市间的直线距离成正比，不妨把两地价格看为是两点间的距离，则由AC2+BC2=AB2可以知道∠ACB是直角．又AD=AC+CD，故A，C，D在一条直线上，即可解出BD的长．
    解答：解：把两地价格看为是两点间的距离，
    则由AC2+BC2=AB2可以知道∠ACB是直角．
    ∴∠BCD是直角，
    ∴BD==1500．
    故答案选A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

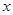    一农民有基本农田2亩，根据往年经验，若种水稻，则每季每亩产量为400公斤；若种花生，则每季每亩产量为100公斤。但水稻成本较高，每季每亩240元，而花生只需80元，且花生每公斤5元，稻米每公斤卖3元。现该农民手头有400元；（1）设该农民种亩水稻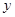，亩花生，利润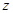元，请写出约束条件及目标函数；（2）问两种作物各种多少，才能获得最大收益？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某厂生产甲产品每千克需用原料A和原料B分别为、千克，生产乙产品每千克需用原料A和原料B分别为、千克。甲、乙产品每千克可获利润分别为、元。月初一次性购进本月用原料A、B各、千克。要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大。在这个问题中，设全月生产甲、乙两种产品分别为千克、千克，月利润总额为元，那么，用于求使总利润最大的数学模型中，约束条件为
    A.   B.   C.  D.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    （文）已知实数x、y满足的最小值是（   ）
    A．2B．5C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设x，y满足约束条件 ，    若目标函数（a>0，b>0）的最大值为12，则的最小值为 (     )
    A．B．C．D．4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若满足约束条件则的最大值为（     ）
    A．3B．10C．6D．9

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    实数的最大值为           ；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知为坐标原点，点的坐标为（），点的坐标、满足不等式组. 若当且仅当时，取得最大值，则的取值范围是
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    .点P（a，3）到直线4x-3y+1=0的距离等于4，且在不等式2x+y-3＜0表示的平面区域内，则点P的坐标是______________.

    查看答案和解析>>

    同步练习册答案