
ШчЭМЃЌвбжЊЧњЯпCЃКyЃНx2(0ЁмxЁм1)ЃЌO(0ЃЌ0)ЃЌQ(1ЃЌ0)ЃЌR(1ЃЌ1)ЃЎШЁЯпЖЮOQЕФжаЕуA1ЃЌЙ§A1зїxжсЕФДЙЯпНЛЧњЯпCгкP1ЃЌЙ§P1зїyжсЕФДЙЯпНЛRQгкB1ЃЌМЧa1ЮЊОиаЮA1P1B1QЕФУцЛ§ЃЎЗжБ№ШЁЯпЖЮOA1ЃЌP1B1ЕФжаЕуA2ЃЌA3ЃЌЙ§A2ЃЌA3ЗжБ№зїxжсЕФДЙЯпНЛЧњЯпCгкP2ЃЌP3ЃЌЙ§P2ЃЌP3ЗжБ№зїyжсЕФДЙЯпНЛA1P1ЃЌRB1гкB2ЃЌB3ЃЌМЧa2ЮЊСНИіОиаЮA2P2B2 A1гыОиаЮA3P3B3B1ЕФУцЛ§жЎКЭЃЎвдДЫРрЭЦЃЌМЧanЮЊ2nЃ1ИіОиаЮУцЛ§жЎКЭЃЌДгЖјЕУЪ§Са{an}ЃЌЩшетИіЪ§СаЕФЧАnЯюКЭЮЊSnЃЎ

(ЃЩ)Чѓa2гыanЃЛ
(Ђђ)ЧѓSnЃЌВЂжЄУїSnЃМ ЃЎ
ЃЎ
(ЃЩ)  ЃЌ
ЃЌ ЃЛЃЈЂђЃЉМћНтЮі.
ЃЛЃЈЂђЃЉМћНтЮі.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈЂёЃЉИљОнЬтвтЯШаДГі ИїЕузјБъЃЌдйЗжБ№Чѓ
ИїЕузјБъЃЌдйЗжБ№Чѓ ЃЌШЛКѓзмНсгыЧњЯп
ЃЌШЛКѓзмНсгыЧњЯп НЛЕузјБъЃЌДгЖјдйЧѓ
НЛЕузјБъЃЌДгЖјдйЧѓ ЃЛЃЈЂђЃЉгЩЃЈЂёЃЉжЊ
ЃЛЃЈЂђЃЉгЩЃЈЂёЃЉжЊ ЕФБэДяЪНЃЌЯШАб
ЕФБэДяЪНЃЌЯШАб БфаЮЮЊВюЕФаЮЪНЃЌдйЧѓ
БфаЮЮЊВюЕФаЮЪНЃЌдйЧѓ БэДяЪНЃЌРћгУЕШБШЪ§СаЧА
БэДяЪНЃЌРћгУЕШБШЪ§СаЧА ЯюКЭЙЋЪНЧѓ
ЯюКЭЙЋЪНЧѓ ЃЌШЛКѓАб
ЃЌШЛКѓАб гы
гы НјааБШНЯЃЌМДЕУжЄ.
НјааБШНЯЃЌМДЕУжЄ.
ЪдЬтНтЮіЃК(ЃЩ) гЩЬтвтжЊP1( ЃЌ
ЃЌ )ЃЌЙЪa1ЃН
)ЃЌЙЪa1ЃН ЁС
ЁС ЃН
ЃН ЃЎ
ЃЎ
гжP2( ЃЌ
ЃЌ )ЃЌP3(
)ЃЌP3( ЃЌ
ЃЌ )ЃЌ
)ЃЌ
ЙЪa2ЃН ЁС[
ЁС[ ЃЋ
ЃЋ Ѓ
Ѓ ]ЃН
]ЃН ЁС(12ЃЋ32Ѓ22)ЃН
ЁС(12ЃЋ32Ѓ22)ЃН ЃЎ
ЃЎ
гЩЬтвтЃЌЖдШЮвтЕФkЃН1ЃЌ2ЃЌ3ЃЌЃЌnЃЌга
 (
( ЃЌ
ЃЌ )ЃЌiЃН0ЃЌ1ЃЌ2ЃЌЃЌ2kЃ1Ѓ1ЃЌ
)ЃЌiЃН0ЃЌ1ЃЌ2ЃЌЃЌ2kЃ1Ѓ1ЃЌ
ЙЪanЃН ЁС[
ЁС[ ЃЋ
ЃЋ Ѓ
Ѓ ЃЋ
ЃЋ Ѓ
Ѓ ЃЋЃЋ
ЃЋЃЋ Ѓ
Ѓ ]
]
ЃН ЁС[12ЃЋ32Ѓ22ЃЋ52Ѓ42ЃЋЁЃЋ(2nЃ1)2Ѓ(2nЃ2)2]
ЁС[12ЃЋ32Ѓ22ЃЋ52Ѓ42ЃЋЁЃЋ(2nЃ1)2Ѓ(2nЃ2)2]
ЃН ЁС{1ЃЋ(4ЁС1ЃЋ1)ЃЋ(4ЁС2ЃЋ1)ЃЋЁЃЋ[4ЁС(2nЃ1Ѓ1)ЃЋ1]}
ЁС{1ЃЋ(4ЁС1ЃЋ1)ЃЋ(4ЁС2ЃЋ1)ЃЋЁЃЋ[4ЁС(2nЃ1Ѓ1)ЃЋ1]}
ЃН ЁС
ЁС
ЃН ЃЎ
ЃЎ
Ыљвдa2ЃН ЃЌanЃН
ЃЌanЃН ЃЌnЁЪN*ЃЎ 10Зж
ЃЌnЁЪN*ЃЎ 10Зж
(Ђђ)гЩ(ЃЩ)жЊanЃН ЃЌnЁЪN*ЃЌ
ЃЌnЁЪN*ЃЌ
ЙЪSnЃН Ѓ
Ѓ ЃН
ЃН Ѓ
Ѓ ЃН
ЃН ЃЎ
ЃЎ
гжЖдШЮвтЕФnЁЪN*ЃЌга ЃО0ЃЌ
ЃО0ЃЌ
ЫљвдSnЃН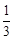
 ЃМ
ЃМ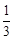 ЃЎ
14Зж
ЃЎ
14Зж
ПМЕуЃК1ЁЂЕнЭЦЙЋЪНЃЛ2ЁЂЕШБШЪ§СаЕФЧАnЯюКЭЙЋЪН.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЧњЯпCЃКy=
ШчЭМЃЌвбжЊЧњЯпCЃКy=| 1 |
| x |
| 1 |
| x+2-n |
| n |
 |
| i=1 |
| 1 |
| 6 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЧњЯпCЃКy=
ШчЭМЃЌвбжЊЧњЯпCЃКy=| 1 |
| x |
| 4 |
| 9 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2006•ФЯОЉЖўФЃЃЉШчЭМЃЌвбжЊЧњЯпCЃКy=
ЃЈ2006•ФЯОЉЖўФЃЃЉШчЭМЃЌвбжЊЧњЯпCЃКy=| 1 |
| x |
| 1 |
| x+2-n |
| 1 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЧњЯпCЃКy=
ШчЭМЃЌвбжЊЧњЯпCЃКy=| 1 |
| x |
| 1 |
| x+2-n |
| 1 |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
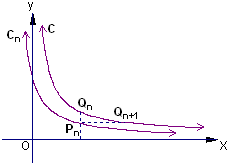
 ШчЭМЃЌвбжЊЧњЯпCЃКy=x2ЃЈ0ЁмxЁм1ЃЉЃЌOЃЈ0ЃЌ0ЃЉЃЌQЃЈ1ЃЌ0ЃЉЃЌRЃЈ1ЃЌ1ЃЉЃЎШЁЯпЖЮOQЕФжаЕуA1ЃЌЙ§A1зїxжсЕФДЙЯпНЛЧњЯпCгкP1ЃЌЙ§P1зїyжсЕФДЙЯпНЛRQгкB1ЃЌМЧa1ЮЊОиаЮA1P1B1QЕФУцЛ§ЃЎЗжБ№ШЁЯпЖЮOA1ЃЌP1B1ЕФжаЕуA2ЃЌA3ЃЌЙ§A2ЃЌA3ЗжБ№зїxжсЕФДЙЯпНЛЧњЯпCгкP2ЃЌP3ЃЌЙ§P2ЃЌP3ЗжБ№зїy жсЕФДЙЯпНЛA1P1ЃЌRB1гкB2ЃЌB3ЃЌМЧa2ЮЊСНИіОиаЮA2P2B2A1гыОиаЮA3P3B3B1ЕФУцЛ§жЎКЭЃЎвдДЫРрЭЦЃЌМЧanЮЊ2n-1ИіОиаЮУцЛ§жЎКЭЃЌДгЖјЕУЪ§Са{an}ЃЌЩшетИіЪ§СаЕФЧАnЯюКЭЮЊSnЃЎ
ШчЭМЃЌвбжЊЧњЯпCЃКy=x2ЃЈ0ЁмxЁм1ЃЉЃЌOЃЈ0ЃЌ0ЃЉЃЌQЃЈ1ЃЌ0ЃЉЃЌRЃЈ1ЃЌ1ЃЉЃЎШЁЯпЖЮOQЕФжаЕуA1ЃЌЙ§A1зїxжсЕФДЙЯпНЛЧњЯпCгкP1ЃЌЙ§P1зїyжсЕФДЙЯпНЛRQгкB1ЃЌМЧa1ЮЊОиаЮA1P1B1QЕФУцЛ§ЃЎЗжБ№ШЁЯпЖЮOA1ЃЌP1B1ЕФжаЕуA2ЃЌA3ЃЌЙ§A2ЃЌA3ЗжБ№зїxжсЕФДЙЯпНЛЧњЯпCгкP2ЃЌP3ЃЌЙ§P2ЃЌP3ЗжБ№зїy жсЕФДЙЯпНЛA1P1ЃЌRB1гкB2ЃЌB3ЃЌМЧa2ЮЊСНИіОиаЮA2P2B2A1гыОиаЮA3P3B3B1ЕФУцЛ§жЎКЭЃЎвдДЫРрЭЦЃЌМЧanЮЊ2n-1ИіОиаЮУцЛ§жЎКЭЃЌДгЖјЕУЪ§Са{an}ЃЌЩшетИіЪ§СаЕФЧАnЯюКЭЮЊSnЃЎ| 1 | 3 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com