
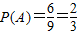 .
.
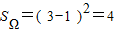 .
. 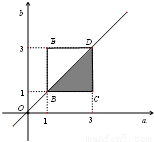 的阴影部分,
的阴影部分,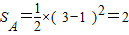 .
. .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:0103 模拟题 题型:解答题
 ,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设
,某植物研究所进行该种子的发芽实验,每次实验种一料种子,每次实验结果相互独立。假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的。若该研究所共进行四次实验,设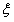 表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;
表示四次实验结束时实验成功的次数与失败的次数之差的绝对值;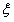 的数学期望E
的数学期望E ;
;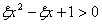 的解集是实数集R”为事件A,求事件A发生的概率P(A)。
的解集是实数集R”为事件A,求事件A发生的概率P(A)。 查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省潮州市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com