分析:当a=0时,由直线方程知b≠0,直线是y轴,与双曲线由两个交点,不和题意.当a≠0时,化一般式为斜截式,和双曲线方程联立后得到关于x的方程,当二次项系数等于0时,直线与双曲线有一个交点,求出a,b的关系,得到直线方程,当二次项系数不等于0时,由判别式等于0,求出b=0,得另一直线的方程.
解答:解:当a=0时,b≠0,直线l:bx+ay-2a=0化为x=0,与双曲线
-+=1有2个公共点,不合题意;
当a≠0时,直线l:bx+ay-2a=0化为y=-
x+2.
联立
,得(9b
2-4a
2)x
2-36abx=0.
若9b
2-4a
2=0,即
=±,方程(9b
2-4a
2)x
2-36abx=0有一解,
即直线l:bx+ay-2a=0与双曲线
-+=1只有一个公共点,
此时直线l的方程为y=-
x+2或y=
x+2;
若9b
2-4a
2≠0,由△=1296a
2b
2=0,得b=0.
此时直线l:bx+ay-2a=0化为y=2,与双曲线
-+=1只有一个公共点;
综上,直线l:bx+ay-2a=0与双曲线
-+=1只有一个公共点的直线l的方程为:
y=2或
y=x+2或
y=-x+2.
故答案为:y=2或
y=x+2或
y=-x+2.
点评:本题考查了直线与圆锥曲线的关系,考查了分类讨论的数学思想方法,训练了利用判别式法分析方程解得个数,解答此题的关键是明确a,b不能同时为0.此题是中档题.



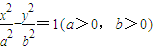 的半焦距为c.已知原点到直线l:bx+ay=ab的距离等于
的半焦距为c.已知原点到直线l:bx+ay=ab的距离等于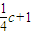 ,则c的最小值为 .
,则c的最小值为 .