
如图,在三棱锥P-ABC中, AB="AC=4," D、E、F分别为PA、PC、BC的中点, BE="3," 平面PBC⊥平面ABC, BE⊥DF.
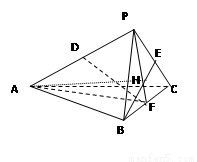
(Ⅰ)求证:BE⊥平面PAF;
(Ⅱ)求直线AB与平面PAF所成的角.
(1)要证明线面垂直关键是对于AF⊥BC垂直的证明,以及平面PBC⊥平面ABC的证明,来得到。
(2)AB与平面PAF所成的角为300.
【解析】
试题分析:解:(Ⅰ)证明:连结AF, ∵ AB="AC," F为BC的中点,
∴ AF⊥BC, ………………( 1 分)
又平面PBC⊥平面ABC, 且平面PBC 平面ABC于BC,
平面ABC于BC,
∴ AF⊥平面PBC. ( 2 分)
又∵ BE 平面PBC,
平面PBC,
∴ AF⊥BE. ( 5 分)
又∵BE⊥DF, DF ,
,
∴ BE⊥平面PAF. ( 5 分)
(Ⅱ)设BE PF="H," 连AH, 由(1)可知AH为AB在平面PAF上的射影,
PF="H," 连AH, 由(1)可知AH为AB在平面PAF上的射影,
所以∠HAB为直线AB与平面PAF所成的角. ( 7分)
∵ E 、F分别为PC、BC的中点,
∴H为△PBC的重心, 又BE=3,
∴BH= ( 9 分)
( 9 分)
在Rt△ABH中, 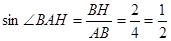 ( 10 分)
( 10 分)
∴AB与平面PAF所成的角为300. (12分)
考点:线面角,线面垂直
点评:解决的关键是利用空间中点线面的位置关系来得到证明,以及结合线面角的定义来的得到求解,属于基础题。


科目:高中数学 来源: 题型:
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
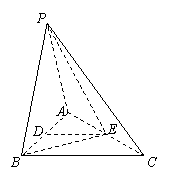

(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求二面角A-PB-E的大小.
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上期中文科数学试卷(解析版) 题型:解答题
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.

(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省内江市、广安市高三第二次模拟联考试题理科数学(解析版) 题型:解答题
如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点。
(1)求证:EF⊥PD;
(2)求直线PF与平面PBD所成的角的大小;
(3)求二面角E-PF-B的大小。

查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高二下学期期中考试数学2-4 题型:解答题
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.

(1)求证AC⊥平面DEF;
(2)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(3)求平面ABD与平面DEF所成锐二面角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com