练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (数学与生产)工厂对某种原料的全年需要量是Q吨．为保证生产，又节省开支，打算全年分若干次等量订购，且每次用完后可立即购进．已知每次订购费用是a元．又年保管费用率是p，它与每次购进的数量(x吨)及全年保管费(S元)之间的关系是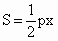．问全年订购多少次才能使订购费用与保管费用之和最少?并求这个最少费用．(为简便计算，不必讨论订购次数是否为整数)

    答案：略
    解析：

    解：设每次购进的数量为x吨，则

    全年定购费，全年保管费，

    定购费与保管费之和．

    由于，

    当且仅当，即时取等号，

    即最优批量订购数为(吨)，

    最小费用数为(元)，

    全年最佳定购次数(次)．

    故全年订购次，才能使全年的订购费用与保管费用之和最少，最少费用元．


    提示：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•成都一模）某工厂在政府的帮扶下，准备转型生产一种特殊机器，生产需要投入固定成本500万 元，年生产与销售均以百台计数，且每生产100台，还需增加可变成本1000万元．若市场对 该产品的年需求量为500台，每生产m百台的实际销售收人近似满足函数R（m）=5000m-500m2（0≤m≤5，m∈N）
    （I）试写出第一年的销售利润y（万元）关于年产量单位x百台，x≤5，x∈N*）的函数关系式；
    （II）若工厂第一年预计生产机器300台，销售后将分到甲、乙、丙三个地区各100台，因技术、运输等原因，估计每个地区的机器中出现故障的概率为
    15
    ．出现故障后，需要厂家上门调试，每个地区调试完毕，厂家需要额外开支100万元．记厂家上门调试需要额外开支的费 用为随机变量ξ，试求第一年厂家估计的利润．
    （说明：销售利润=实际销售收入一成本；估计利润=销售利润一ξ的数学期望）

    查看答案和解析>>

    同步练习册答案