
分析 将已知化为:$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$的形式,判断x+y+z=1是否成立,可得P与点A,B,C是否共面.
解答 解:(1)∵$\overrightarrow{OA}$$+2\overrightarrow{OB}$=6$\overrightarrow{OP}$$-3\overrightarrow{OC}$,
∴6$\overrightarrow{OP}$=$\overrightarrow{OA}$$+2\overrightarrow{OB}$+$3\overrightarrow{OC}$,
∴$\overrightarrow{OP}$=$\frac{1}{6}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$,
∵$\frac{1}{6}$+$\frac{1}{3}$+$\frac{1}{2}$=1,
∴P与点A,B,C共面;
(2)∵$\overrightarrow{OP}$$+\overrightarrow{OC}$=4$\overrightarrow{OA}$-$\overrightarrow{OB}$.
∴$\overrightarrow{OP}$=4$\overrightarrow{OA}$-$\overrightarrow{OB}$-$\overrightarrow{OC}$.
∵4-1-1≠0,
∴P与点A,B,C不共面.
点评 本题考查的知识点是共面向量,正确理解并熟练掌握四点共面充要条件的向量表示,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 1或-2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
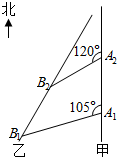 如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里?
如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.
如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com