
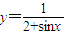 的值域为 ,
的值域为 ,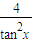 +1≥4+1=5,当且仅当tanx=
+1≥4+1=5,当且仅当tanx=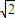 时取等号,得到y的最小值为5,所以得到y的值域.
时取等号,得到y的最小值为5,所以得到y的值域. ≤
≤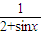 ≤1即
≤1即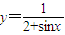 的值域为[
的值域为[ ,1];
,1];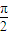 ,
,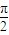 ],所以y=cos(sinx)的值域为[cos1,1];
],所以y=cos(sinx)的值域为[cos1,1];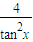 +1≥4+1=5,当且仅当tanx=
+1≥4+1=5,当且仅当tanx=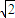 时取等号,所以y=tan2x+4cot2+1的值域为[5,+∞).
时取等号,所以y=tan2x+4cot2+1的值域为[5,+∞). ,1],(2)[cos1,1],(3)[5,+∞)
,1],(2)[cos1,1],(3)[5,+∞)

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 | 20 |
| y1 | y2 | 合计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合计 | a+c | b+d | a+b+c+d |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
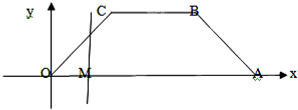 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.| 7 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
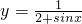 的值域为 ______,
的值域为 ______,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com