分析:根据集合M有8个子集,可以判断出集合M中共有3个元素,即|x2-2x|+a=0有3个根,转化为y=|x2-2x|与y=-a的图象有三个交点,画出图象即可解得a的值.
解答:解:∵集合M={x||x
2-2x|+a=0}有8个子集,根据集合中有n个元素,则集合有2
n个子集,
∴2
n=8,解得,n=3,
∴集合M={x||x
2-2x|+a=0}中有3个元素,即|x
2-2x|+a=0有3个根,
∴函数y=|x
2-2x|与y=-a的图象有三个交点,
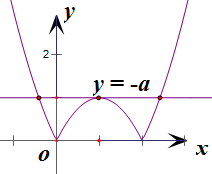
作出y=|x
2-2x|与y=-a的图象如右图所示,
∴实数a的值a=-1.
故答案为:-1.
点评:本题考查了集合的子集个数以及函数的零点.如果集合中有n个元素,则集合有2n个子集.对于方程的根问题,可以运用数形结合的思想转化为两个图象的交点的问题进行解决.属于中档题.



